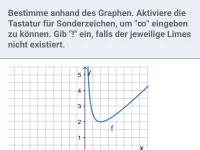
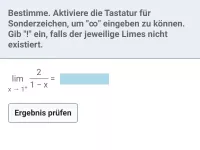
Was bedeutet der Limes von f(x) für x → c− bzw. x → c+?

Sei c eine beliebige reelle Zahl. Der Limes von f(x) für x → c− bzw. x → c+ gibt an, wie sich die Funktion in unmittelbarer Umgebung links bzw. rechts von x = c verhält.

Beispiel
Wie verhält sich f in der Umgebung der Definitionslücken?
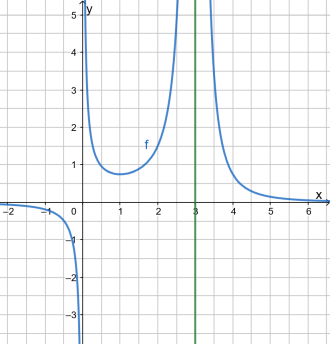
graphik
Lösung:
lim
x → 0−
 
f(x)
=
−
∞
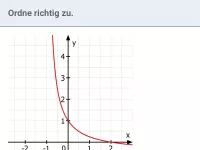
Begründung: y wird beliebig klein (Graph geht unbeschränkt nach unten), wenn man der Stelle x = 0 (y-Achse) von links nur nahe genug kommt.
lim
x → 0+
 
f(x)
=
∞
Begründung: y wird beliebig groß (Graph geht unbeschränkt nach oben), wenn man der Stelle x = 0 (y-Achse) von rechts nur nahe genug kommt.
lim
x → 3−
 
f(x)
=
lim
x → 3+
 
f(x)
=
∞
Begründung: y wird beliebig groß (Graph geht unbeschränkt nach oben), wenn man der Stelle x = 3 von links oder von rechts nur nahe genug kommt.
lim
x → 4
 
f(x)
=
f
 
4
Begründung: y nähert sich dem Funktionswert an der Stelle 4 beliebig an, wenn x nur nah genug bei 4 liegt.

Merke:
  • ±∞ als Limes ergibt sich immer dann, wenn sich der Graph an der betrachteten Stelle einer senkrechten Asymptote annähert.
  • Ein Zahlenwert als Limes ergibt sich immer dann, wenn sich der Graph an der betrachteten Stelle "normal" verhält (wie hier) oder wenn er ein "Loch" aufweist.
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen