Was sind Polstellen bei gebrochen-rationalen Funktionen und wie verhält sich der Graph in ihrer Umgebung?
Polstellen sind spezielle Definitionslücken. In der Umgebung einer Polstelle
- wächst der Funktionswert betragsmäßig ins Unendliche
- schmiegt sich der Graph folglich an eine senkrechte Asymptote an
- mit Vorzeichenwechsel (+/− oder −/+) oder
- ohne Vorzeichenwechsel(+/+ oder −/−).
Beispiel
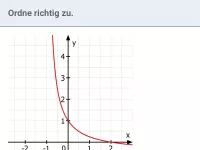
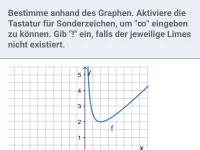
Lies aus dem Graphen evtl. auftretende Null- und Polstellen ab und charakterisiere diese näher.

Da der Graph die x-Achse bei
schneidet, liegt hier eine Nullstelle vor.
x | = |
|
Da der Graph sich bei
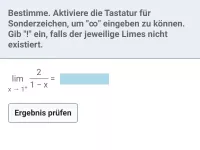
einer senkrechten Asymptoten annähert, liegt hier eine Polstelle vor. Links von der Asymptote geht der Graph "unendlich weit" nach unten (−∞), rechts davon ebenso (−∞). Also handelt es sich um eine Polstelle der Art −/−. Insbesondere liegt kein Vorzeichenwechsel (VZW) vor.
x | = |
|
Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
- Wie bestimmt und spezifiziert man eine Polstelle in der Mathematik?
- Was versteht man unter einer behebbaren Definitionslücke?
- Was bedeutet der Limes von f(x) für x → c− bzw. x → c+?
- Was passiert mit einem Bruch, wenn der Zähler konstant ≠ 0 ist und der Nenner gegen 0 strebt?
- Wie bestimmt man das Verhalten einer gebrochen-rationalen Funktion für x gegen Unendlich?
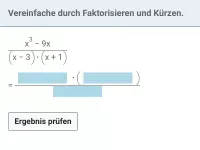
- Wie lassen sich Bruchterme vereinfachen und welche Techniken sind dabei hilfreich?