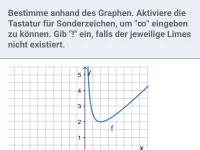
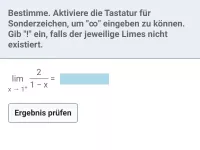
Wie bestimmt und spezifiziert man eine Polstelle in der Mathematik?

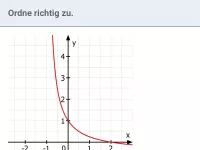
Um eine Polstelle x0 zu spezifizieren, muss man die einseitigen Grenzwerte bestimmen. Dazu lässt man x einmal von links gegen x0 gehen und einmal von rechts.

Beispiel: x0=1
"von links gegen 1" trifft etwa auf die Folge 0,9 ; 0,99 ; 0,999 ... zu.
"von rechts gegen 1" trifft etwa auf die Folge 1,1 ; 1,01 ; 1,001 ... zu.

Oft erkennt man schon ohne direktes Ausrechnen, ob der Funktionswert f(x) sich dabei gegen +∞ oder −∞ entwickelt.

Beispiel
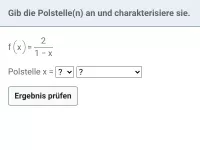
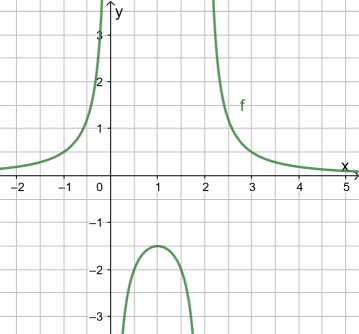
Bestimme alle auftretenden Polstellen und charakterisiere diese näher
3
2x
2
−
4x
Lösung:
3
2x
2
−
4x
=
3
2x
 
x
−
2
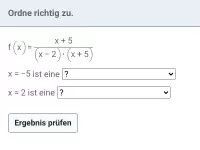
Der Nenner weist genau zwei Nullstellen und damit Polstellen der Funktion, nämlich 
x
1
=
0
 und 
x
2
=
2
 auf. Da es sich jeweils um einfache Nullstellen handelt (die entsprechenden Faktoren stehen in der ersten Potenz), sind beide Polstellen jeweils mit Vorzeichenwechsel. Für die genauere Untersuchung bestimmt man die einseitigen Limites:
lim
x→0−
 
3
2x
·
1
x
−
2
=
"
 
3
0−
·
1
−
2
 
"
=
"
 
−
∞
·
−
1
2
 
"
=
∞
Analog könnte man den Limes für 
x→0+
 bestimmen, aber da man oben festgestellt hat, dass hier eine Polstelle mit VZW vorliegt, hat man bereits damit gezeigt, dass es sich bei 
x
1
=
0
 um eine Polstelle der Art +/− handeln muss.
lim
x→2−
 
3
2x
·
1
x
−
2
=
"
 
3
4
·
1
0−
 
"
=
"
 
3
4
·
−
∞
 
"
=
−
∞
Mit demselben Argument wie oben kann man bereits hier feststellen, dass es sich bei 
x
2
=
2
 um eine Polstelle der Art −/+ handelt.
graphik
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen