Was sind die Erkennungsmerkmale ähnlicher Dreiecke?
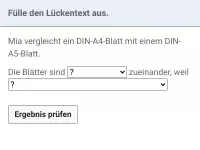
Zwei Dreiecke können unterschiedlich groß sein und doch ähnlich aussehen, weil sie dieselben Proportionen (Seitenverhältnisse) haben.
Ähnlich sind zwei Dreiecke dann, wenn sie ... übereinstimmen.
- im Längenverhältnis sich entsprechender Seiten (S:S:S-Satz)
- in zwei Winkeln (W:W-Satz)
- in einem Winkel und dem Längenverhältnis der anliegenden Seiten (S:W:S-Satz)
- im Längenverhältnis zweier sich entsprechender Seiten und dem Winkel gegenüber der längeren Seite (S:s:W-Satz)
Beispiel
Gegeben sind die Dreiecke ABC und DEF mit
Sind beide Dreiecke ähnlich und wenn ja nach welchem Satz?
γ | = | 45°, |
a | = | 1, |
b | = | 2, |
δ | = | 45°, |
d | = | 4, |
e | = | 2. |
Skizze:
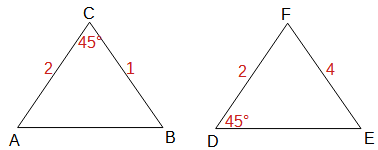
Wie man in der Skizze erkennt, stimmen beide Dreiecke zwar in einem Winkel und auch im Verhältnis zweier Seiten überein (in jedem Dreieck ist eine Seite doppelt so groß wie die andere), allerdings liegen im Dreieck die betreffenden Seiten am 45°-Winkel an, während im Dreieck DEF die Seite mit der Länge 4 nicht anliegt. Daher kann der S:W:S hier nicht angewendet werden. Die Frage, ob beide Dreiecke ähnlich sind, lässt sich ohne weitere Information oder Überlegung also nicht beantworten.
Siehe auch