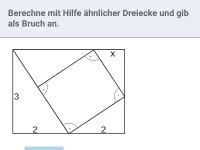
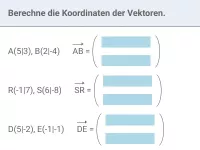
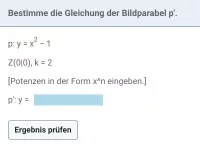
Was sind die Eigenschaften ähnlicher Dreiecke?
Zwei Figuren sind ähnlich, wenn sie in den jeweils entsprechenden Winkeln und allen Seitenverhältnissen entsprechender Seiten übereinstimmen. Dieses Verhältnis wird als Streckungsfaktor (oder Ähnlichkeitsfaktor) k bezeichnet; k drückt aus, wie lang die Seiten in Figur 2 im Vergleich zu den entsprechenden Seiten in Figur 1 sind. Z.B. bedeutet k=0,5, dass Figur 2 längenmäßig halb so groß wie Figur 1 ist.
- Kennt man k, so kann man zu jeder Seitenlänge in Figur 1 durch Multiplikation mit k die entsprechende Seitenlänge in Figur 2 angeben.
- Kennt man die Längen von zwei sich entsprechenden Seiten in Figur 1 und Figur 2, so kann man k durch Division der Seitenlängen "Figur 2 : Figur 1" bestimmen.
Beispiel
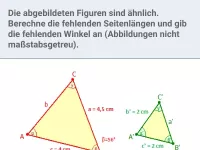
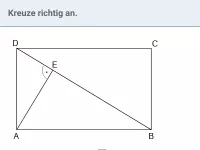
Die beiden Figuren sind ähnlich. Berechne die fehlenden Seitenlängen und gib die fehlenden Winkel an (Abbildungen nicht maßstabsgetreu).
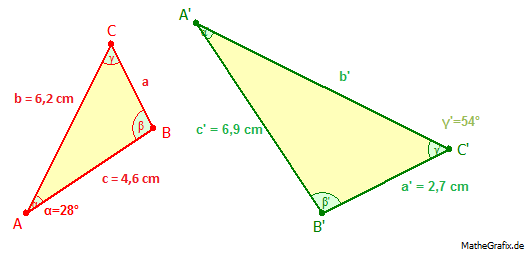
a | = | ? |
β | = | ? |
γ | = | ? |
b' | = | ? |
| = | ? |
| = | ? |
- Winkel
Da die Dreiecke ähnlich sind, stimmen sie in allen Winkeln überein. Also:
|
|
Mithilfe der Winkelsumme im Dreieck erhält man dann:
| = | 98 |
|
|
- Streckenlängen
Teilt man die Seitenlänge c' = 6,9 cm durch die Seitenlänge c = 4,6 cm, erhält man den Streckfaktor k:
| = | 1,5 |
Streckfaktor k = 1,5.
b' bekommt man, indem man b = 6,2 cm mit dem Streckfaktor k multipliziert:
| = |
|
a erhält man, wenn man a' = 2,7 cm durch den Streckfaktor k teilt:
| = |
|
Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
- Was sind die Erkennungsmerkmale ähnlicher Dreiecke?
- Wie ermittelt man den Vektor einer einzelnen Parallelverschiebung, die zwei hintereinanderfolgenden Parallelverschiebungen entspricht?
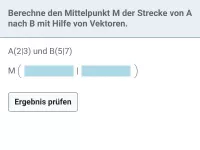
- Wie berechnet man den Mittelpunkt einer Strecke AB?
- Wie wirkt sich eine zentrische Streckung auf Länge und Richtung eines Vektors aus und wie berechnet man die Koordinaten des Bildvektors?
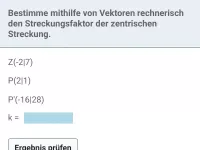
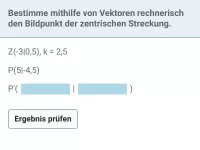
- Wie bestimmt man bei einer zentrischen Streckung den Punkt P, den Bildpunkt P' oder den Streckungsfaktor k mit Vektoren?
- Wie erhältst du die Gleichung einer Bildgerade oder Bildparabel bei einer zentrischen Streckung, wenn die Urgerade bzw. Urparabel durch ihre Gleichung gegeben sind?