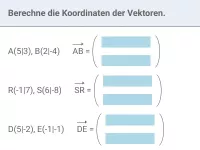
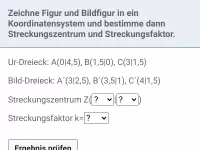
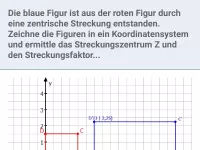
Wie wirkt sich eine zentrische Streckung auf Länge und Richtung eines Vektors aus und wie berechnet man die Koordinaten des Bildvektors?
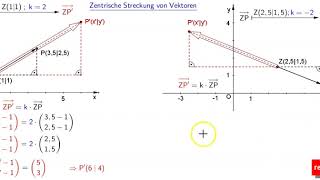
Streckt man einen Vektor durch zentrische Streckung mit dem Streckungsfaktor k, dann erhält man die Koordinaten des Bildvektors, indem man die Koordinaten des Urvektors jeweils mit k multipliziert. Es gilt:
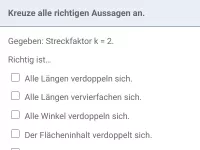
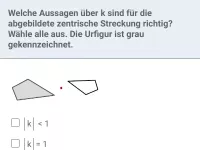
- Der Bildvektor ist |k|-mal so lang wie der Urvektor
- k>0: Ur- und Bildvektor haben die gleiche Richtung
- k<0: Ur- und Bildvektor haben gegensätzliche Richtungen
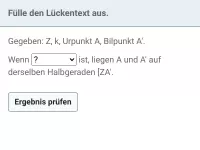
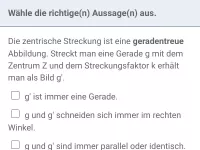
- Bild- und Urvektor sind immer parallel zueinander (oder identisch)
Beispiel
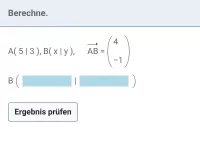
AB
| = |
|
a)
k | = | 0,5 |
b)
k | = |
|
zentrisch gestreckt werden. Bestimme jeweils den Bildvektor
und beschreibe sein Aussehen im Vergleich zum Urvektor.
A'B'
Zu a)
| = |
|
Der Bildvektor ist halb so lang wie der Urvektor, parallel zu ihm und zeigt in die gleiche Richtung (k positiv).
Zu b)
| = |
|
Der Bildvektor ist doppelt lang wie der Urvektor, parallel zu ihm und zeigt in die entgegengesetzte Richtung (k negativ).
Lernvideo
Zentrische Streckung von Vektoren
Kanal: realmathde
Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
-
≈7. Klasse - Aufgaben + Stoff + Video
Vektoren (zweidimensional)
Vektorkoordinaten berechnen, Rechnen mit Vektoren, Parallelverschiebung -
≈8. Klasse - Aufgaben + Stoff + Video
Zentrische Streckung
Zentrische Streckung einer Figur bei gegebenem Zentrum Z und Streckungsfaktor k. Ermittlung von Z und k anhand gegebener Figur und Bildfigur; Eigenschaften der zentrischen Streckung
Ähnliche Themen
- Wie ermittelt man den Vektor einer einzelnen Parallelverschiebung, die zwei hintereinanderfolgenden Parallelverschiebungen entspricht?
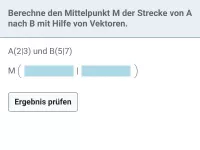
- Wie berechnet man den Mittelpunkt einer Strecke AB?
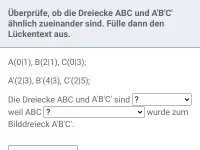
- Was sind die Eigenschaften ähnlicher Dreiecke?
- Was ist eine zentrische Streckung und welche Eigenschaften sowie Auswirkungen hat der Streckungsfaktor k?
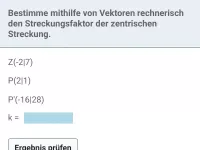
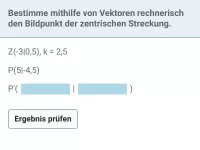
- Wie bestimmt man bei einer zentrischen Streckung den Punkt P, den Bildpunkt P' oder den Streckungsfaktor k mit Vektoren?
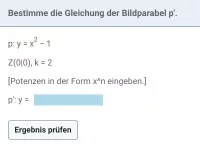
- Wie erhältst du die Gleichung einer Bildgerade oder Bildparabel bei einer zentrischen Streckung, wenn die Urgerade bzw. Urparabel durch ihre Gleichung gegeben sind?