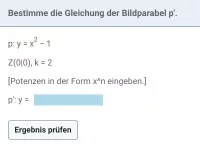
Was ist eine zentrische Streckung und welche Eigenschaften sowie Auswirkungen hat der Streckungsfaktor k?
Zentrische Streckung
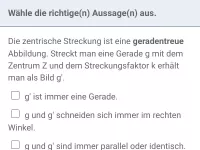
Die Zentrische Streckung ist eine Ähnlichkeitsabbildung. Eine Figur wird im gegebenen Verhältnis vergrößert oder verkleinert (oder bleibt gleich). Dabei gilt:
- Alle Streckenpaare von Urfigur und Bildfigur sind jeweils parallel (oder identisch).
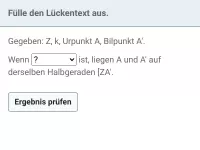
- Streckungszentrum Z, Urpunkt und Bildpunkt liegen auf einer Geraden (hilfreich für die Konstruktion!).
- Die Form der Figur verändert sich nicht, insbesondere bleiben alle Winkelmaße gleich groß.
- Der Streckungsfaktor k gibt das Maß der Vergrößerung/Verkleinerung an und berechnet sich als Quotient aus Bildstreckenlänge und Ausgangsstreckenlänge, z.B. |k |=| ZA'| : |ZA|.
Was uns der Streckfaktor k sagt...:
- k positiv ⇒ Urfigur und Bildfigur liegen auf derselben Seite von Z.
- k negativ ⇒ Urfigur und Bildfigur liegen auf unterschiedlichen Seiten von Z.
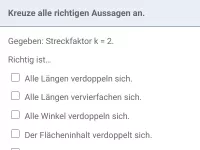
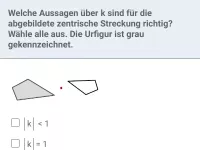
- |k| > 1 ⇒ Bildfigur ist vergrößert.
- |k| < 1 ⇒ Bildfigur ist verkleinert.
- Bildstrecke ist |k| - fach so lang wie die Ursprungsstrecke.
- Flächeninhalt der Bildfigur ist k2 so groß wie Flächeninhalt der Urfigur.
Beispiel 1
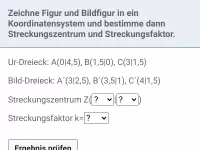
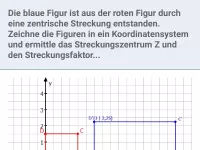
Die blaue Figur ist aus der roten Figur durch eine zentrische Streckung entstanden. Zeichne die Figuren in ein Koordinatensystem und ermittle das Streckungszentrum Z und den Streckungsfaktor k.
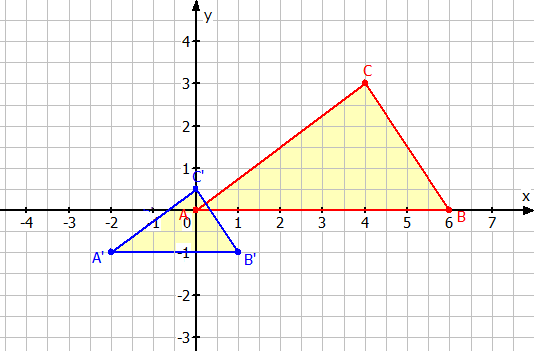
Z |
|
k=?
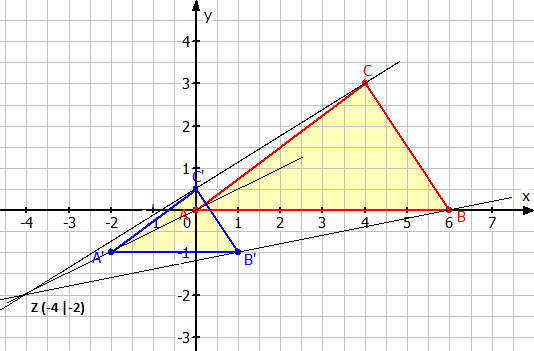
- Streckungszentrum Z:
Zeichnet man Hilfslinien durch die einander entsprechenden Eckpunkte der zwei Dreiecke, schneiden sich diese in einem Punkt, dem Streckungszentrum Z. Aus der Zeichnung liest man ab:
|
- Streckungsfaktor k:
Um den Streckungsfaktor zu berechnen, teilt man die Länge einer Seite des blauen Dreiecks durch die Länge der entsprechenden Seite des roten Dreiecks:
| = | 0,5 |
k | = |
|
Beispiel 2
Strecke das Viereck ABCD am Streckungszentrum Z mit Streckungsfaktor k.
A |
|
B |
|
C |
|
D |
|
Streckungszentrum:
Z |
|
Streckfaktor:
k | = | 2 |
Gib die Koordinaten der gestreckten Figur an.
Zeichne die Figur mit den angegebenen Koordinaten und das Streckungszentrum in ein Koordinatensystem ein.
Zeichne eine Hilfslinie vom Streckungszentrum Z durch den Eckpunkt A der Urfigur.
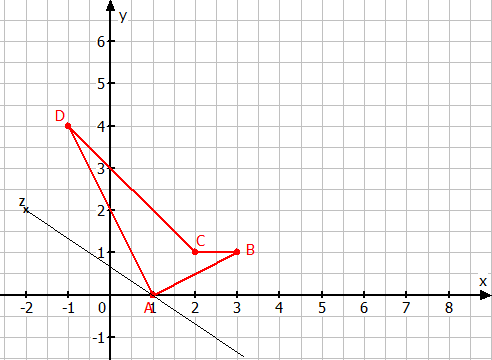
Miss die Länge der Strecke
.
ZA
|
Trage von Z aus das Doppelte dieser Länge an der Hilfslinie ab (allgemein: das |k|-fache). Markiere den Bildpunkt A'.
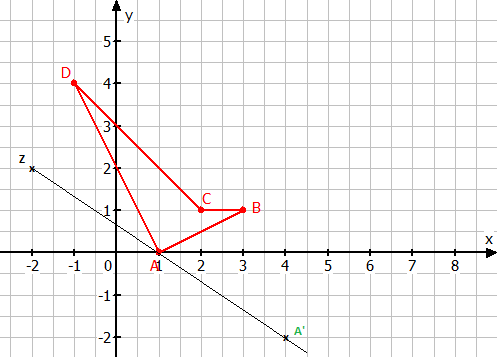
Wiederhole das Vorgehen für alle Eckpunkte der Urfigur und verbinde die Bildpunkte der Reihe nach.
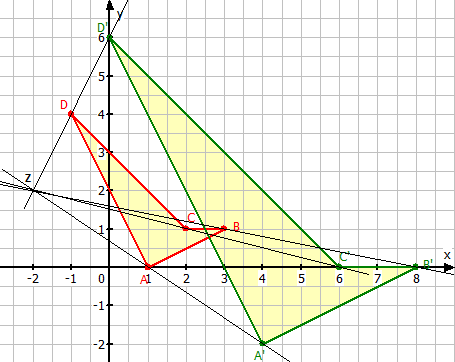
Die Koordinaten der Bildfigur sind:
A' |
|
B' |
|
C' |
|
D' |
|
Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
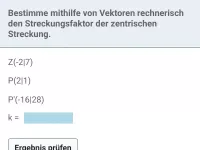
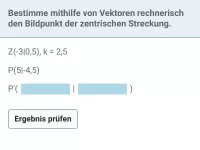
- Wie wirkt sich eine zentrische Streckung auf Länge und Richtung eines Vektors aus und wie berechnet man die Koordinaten des Bildvektors?
- Wie bestimmt man bei einer zentrischen Streckung den Punkt P, den Bildpunkt P' oder den Streckungsfaktor k mit Vektoren?
- Wie erhältst du die Gleichung einer Bildgerade oder Bildparabel bei einer zentrischen Streckung, wenn die Urgerade bzw. Urparabel durch ihre Gleichung gegeben sind?