Wie kann man den Kehrsatz einer mathematischen Aussage leicht formulieren?
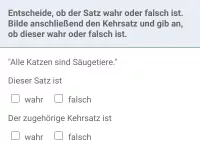
Zu einer Aussage mit Voraussetzung und Behauptung kann man den Kehrsatz formulieren, indem man Voraussetzung und Behauptung miteinander vertauscht.
Das gelingt oft leichter, wenn man ...
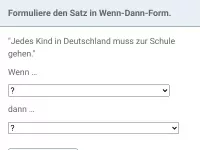
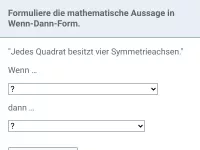
- den ursprünglichen Satz zuerst in die Wenn-Dann-Form bringt,
- dann den Wenn-Teil und den Dann-Teil miteinander vertauscht
- und (falls gewünscht) den so erhaltenen Kehrsatz möglichst einfach formuliert.
Beispiel
Formuliere zum folgenden Satz den Kehrsatz:
"Jedes Viereck mit vier gleich langen Seiten ist eine Raute."
- Voraussetzung:
- Behauptung:
- Wenn-Dann-Form:
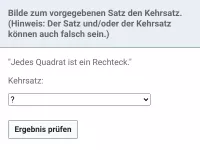
- Kehrsatz in Wenn-Dann-Form:
- Kehrsatz in Kurzform:
Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
- Welche Struktur liegt jeder mathematischen Aussage zugrunde und wie kann man diese durch Umformulierung verdeutlichen?
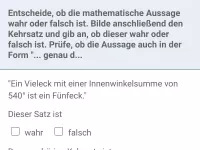
- Wann verwendet man die Formulierung "...genau dann..., wenn..." in der Mathematik und wie ist der Wahrheitsgehalt von Satz und Kehrsatz?
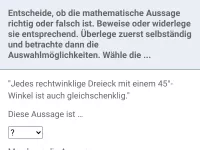
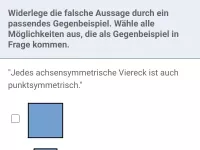
- Wie beweist man eine mathematische Aussage oder widerlegt sie? Welche fünf Strategien gibt es dafür?