Welche Struktur liegt jeder mathematischen Aussage zugrunde und wie kann man diese durch Umformulierung verdeutlichen?
Manche Sätze der Alltagssprache und alle mathematischen Aussagen besitzen eine (manchmal versteckte) Struktur:
- Einerseits geben sie an, unter welcher Bedingung oder für welche Objekte oder in welchen Fällen sie eine Aussage treffen. Das ist die Voraussetzung.
- Außerdem enthalten sie natürlich die eigentliche Behauptung.
- Der Wenn-Teil enthält die Voraussetzung.
- Der Dann-Teil enthält die Behauptung.
Beispiel 1
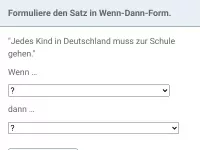
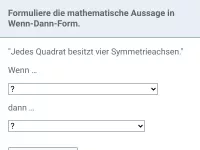
Gib die Voraussetzung und die Behauptung an und bringe den Satz in die Wenn-Dann-Form:
"Radfahrer bis 10 Jahren dürfen den Gehweg benutzen."
Voraussetzung: Ein Radfahrer ist höchstens 10 Jahre alt.
Behauptung: Er darf den Gehweg benutzen.
Wenn-Dann-Form: Wenn ein Radfahrer höchstens 10 Jahre alt ist, dann darf er den Gehweg benutzen.
Beispiel 2
Gib die Voraussetzung und die Behauptung an und bringe den Satz in die Wenn-Dann-Form:
"Jedes achsensymmetrische Dreieck besitzt zwei übereinstimmende Innenwinkel."
Voraussetzung: Ein Dreieck ist achsensymmetrisch.
Behauptung: Zwei Innenwinkel stimmen überein.
Wenn-Dann-Form: Wenn ein Dreieck achsensymmetrisch ist, stimmen zwei Innenwinkel überein.
Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
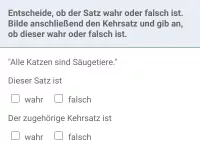
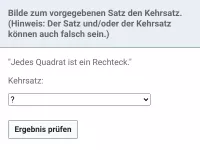
- Wie kann man den Kehrsatz einer mathematischen Aussage leicht formulieren?
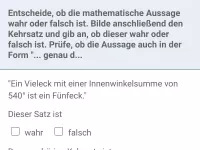
- Wann verwendet man die Formulierung "...genau dann..., wenn..." in der Mathematik und wie ist der Wahrheitsgehalt von Satz und Kehrsatz?
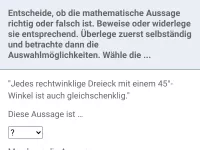
- Wie beweist man eine mathematische Aussage oder widerlegt sie? Welche fünf Strategien gibt es dafür?