Was sind Grenzverteilung und Grenzmatrix in stochastischen Prozessen?
Grenzverteilung und Grenzmatrix
Wenn sich ein stochastischer Prozess mit wachsender Zahl n an Wiederholungen stabilisiert, so erreicht der stochastische Prozess eine Grenzverteilung g, die sich durch Multiplikation mit der Übergangsmatrix U nicht mehr ändert, d.h.:
U·g = g
Das Grenzverhalten wird auch durch die Grenzmatrix G beschrieben. Die Grenzmatrix wird mit dem GTR berechnet, indem für immer größer werdende n die Potenzen Un der Übergangsmatrix berechnet werden, bis sich ein stabilisierender Effekt ablesen lässt.
Das Grenzverhalten ist vom Startvektor abhängig, wenn der stochastische Prozess absorbierende Zustände enthält. Ansonsten gibt es nur genau eine Grenzverteilung.
Beispiel 1
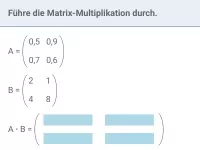
Ein stochastischer Prozess ist gegeben durch Übergangsmatrix U und Startzustand |
|
U | = |
|
| = |
|
| : |
G | = | ? |
g
| = | ? |
Lösung:
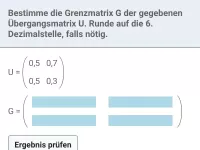
- Bestimmung der Grenzmatrix
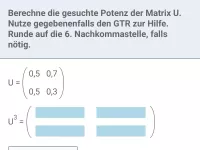
Wir berechnen mit dem GTR einige Potenzen von U, um ein stabilisierendes Verhalten erkennen zu können:
| = |
|
| = |
|
| = |
|
| = |
|
| = |
|
| = |
|
| = |
|
|
- Bestimmung der Grenzverteilung
g
| = |
|
g
| = |
|
|
Das heißt, auf lange Sicht werden sich etwa 36,4% in Zustand 1 und 63,6% in Zustand 2 befinden.
Beispiel 2
Überprüfe, ob die gegebenen Verteilungen Grenzverteilungen der Matrix U sind:
U | = |
|
| = |
|
| = |
|
Für jede Grenzverteilung gilt:
| = | g
|
|
|
| = |
|
| KEINE Grenzverteilung von U. |
|
|
| = |
|
| Grenzverteilung von U. |
Siehe auch