Wie funktioniert die Multiplikation von quadratischen Matrizen?

Matrizen-Multiplikation

Zwei quadratische Matrizen können miteinander multipliziert werden. Das Ergebnis ist wieder eine quadratische Matrix.

Zum Multiplizieren zweier Matrizen müssen die Zeilenvektoren der ersten Matrix mit den Spaltenvektoren der zweiten Matrix multipliziert werden. Der Eintrag in der m-ten Zeile und n-ten Spalte der Produktmatrix ist das Ergebnis des Skalarprodukts aus Zeile m der ersten Matrix und Spalte n der zweiten Matrix.

Spezialfall: Insbesondere können auch Potenzen einer quadratischen Matrix berechnet werden. Dies wird bei der Berechnung von Zustandsverteilungen interessant.

Es gilt: Die Potenz einer stochastischen Matrix ist wieder eine stochastische Matrix.

Beispiel 1
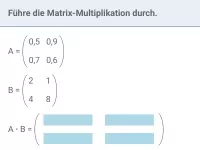
Berechne die Produktmatrix aus A und B:
A
=
0,3
0,7
 
 
 
0,4
0,6
B
=
0,2
0,8
 
 
 
0,1
0,9
A
·
B
=
?
Lösung:
  • Exemplarische Berechnung des ersten Eintrags
A
·
B
=
0,3
0,7
 
 
 
0,4
0,6
·
0,2
0,8
 
 
 
0,1
0,9
=
0,3
·
0,2
+
0,4
·
0,8
…
 
 
 
 
 
 
 
…
…
=
0,38
…
 
 
 
 
 
 
 
…
…
  • Berechnung der restlichen Einträge
A
·
B
=
0,3
0,7
 
 
 
0,4
0,6
·
0,2
0,8
 
 
 
0,1
0,9
A
·
B
=
0,38
0,7
·
0,2
+
0,6
·
0,8
 
 
 
 
 
 
 
 
 
 
0,3
·
0,1
+
0,4
·
0,9
0,7
·
0,1
+
0,6
·
0,9
A
·
B
=
0,38
0,62
 
 
 
 
 
 
 
 
0,39
0,61
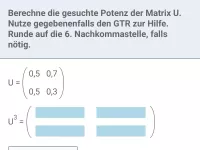
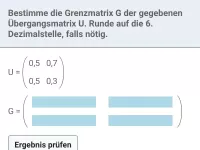
Beispiel 2
Ein stochastischer Prozess ist gegeben durch Übergangsmatrix U und Startzustand
 
v
0
U
=
0,3
0,7
 
 
 
0,4
0,6
v
0
=
1
0
Bestimme die Zustandsverteilung
 
v
3
 
auf zwei Methoden.
Lösung:
  • Berechnung Schritt für Schritt
Allgemein gilt:
 
v
k
+
1
=
U
·
v
k
Also:
v
1
=
U
·
v
0
v
1
=
0,3
0,7
 
 
 
0,4
0,6
·
1
0
v
1
=
0,3
0,7
v
2
=
U
·
v
1
v
2
=
0,3
0,7
 
 
 
0,4
0,6
·
0,3
0,7
v
2
=
0,3
·
0,3
+
0,4
·
0,7
0,7
·
0,3
+
0,6
·
0,7
v
2
=
0,37
0,63
v
3
=
U
·
v
2
v
3
=
0,3
0,7
 
 
 
0,4
0,6
·
0,37
0,63
v
3
=
0,3
·
0,37
+
0,4
·
0,63
0,7
·
0,37
+
0,6
·
0,63
v
3
=
0,363
0,637
  • Berechnung mit einer Matrix-Potenz
Allgemein gilt:
 
v
n
=
U
n
·
v
0
Also:
v
3
=
U
3
·
v
0
v
3
=
0,3
0,7
 
 
 
0,4
0,6
3
·
1
0
v
3
=
0,363
0,637
 
 
 
0,364
0,636
·
1
0
v
3
=
0,363
0,637
Bemerkung: Du solltest beide Methoden beherrschen. Allerdings ist die Berechnung Schritt für Schritt nur für wenige Fälle geeignet. Bei größerer Schrittzahl macht nur die Berechnung mit dem GTR über die Matrix-Potenz Sinn.
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen