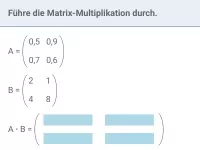
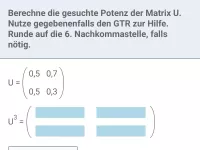
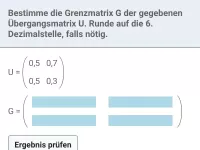
Was ist eine inverse Matrix und welche Eigenschaft ergibt sich bei ihrer Multiplikation mit der Ursprungsmatrix?

Inverse Matrix

Die inverse Matrix zu einer quadratischen Matrix U wird mit U−1 bezeichnet.

Das Produkt aus einer Matrix und ihrer Inversen ergibt die Einheitsmatrix, die in der Diagonale die Einträge 1 und ansonsten nur die Einträge 0 besitzt.

Mit einer inversen Matrix können Zustandsverteilungen in der Vergangenheit berechnet werden, denn aus vk+1 = U · vk folgt: vk = U−1 · vk+1

Beispiel
Ein stochastischer Prozess zwischen drei Zuständen ist durch folgende Übergangsmatrix gegeben:
U
=
0,3
0,7
0
 
 
 
0
0,65
0,35
 
 
 
0
0
1
v
k
 
sei die Zustandsverteilung nach k Schritten.
Ist-Zustand: 15% in Zustand A, 48% in Zustand B, 37% in Zustand C
Bestimme mit Hilfe der inversen Matrix die Zustandsverteilung einen Schritt vorher.
Lösung:
  • Bestimmung der gegebenen Zustandsverteilung:
Ist-Zustand, wir nennen ihn Zustand 1: 15% in Zustand A, 48% in Zustand B, 37% in Zustand C, daher:
v
1
=
0,15
0,48
0,37
  • Zusammenhang der gegebenen und gesuchten Zustandsverteilung:
Allgemein gilt:
v
k
+
1
=
U
·
v
k
Und daher:
v
1
=
U
·
v
0
v
1
 
ist gegeben, für
 
v
0
 
(Zustandsverteilung einen Schritt vorher) setzen wir Variablen ein. Das ergibt:
0,15
0,48
0,37
=
0,3
0,7
0
 
 
 
0
0,65
0,35
 
 
 
0
0
1
·
a
b
c
  • Aufstellen und Lösen der Umkehr-Gleichung:
Die Umkehrgleichung lautet:
0,3
0,7
0
 
 
 
0
0,65
0,35
 
 
 
0
0
1
−
1
·
0,15
0,48
0,37
=
a
b
c
Der GTR liefert:
a
b
c
=
0,3
0,7
0
 
 
 
0
0,65
0,35
 
 
 
0
0
1
−
1
·
0,15
0,48
0,37
a
b
c
=
0,5
0,2
0,3
Einen Schritt vorher waren 50% in Zustand A, 20% in Zustand B und 30% in Zustand C.
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen