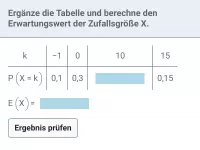
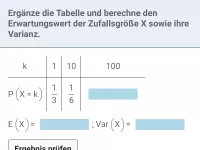
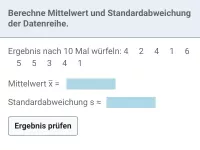
Die Varianz Var(X) einer Zufallsgröße X gibt grob gesagt an, wie stark die Werte einer Zufallsgröße vom Erwartungswert abweichen. Um sie zu berechnen, muss man zunächst den Erwartungswert μ bestimmen. Für jeden Wert k, den X annehmen kann, ist dann folgende Rechnung durchzuführen:
Die Summe dieser Produkte (für alle k) ergibt die Varianz, also
Var(X) = Σ (k − μ)2· P(X = k)
Alternativ kann die Varianz berechnet werden über die "Verschiebungsformel":
Var(X) = E(X2) - E(X)2
Var(X) = (Σ k2· P(X = k)) - μ2
- den Erwartungswert μ abziehen
- Ergebnis quadrieren
- Ergebnis mit zugehöriger Wahrscheinlichkeit multiplizieren
Die Summe dieser Produkte (für alle k) ergibt die Varianz, also
Var(X) = Σ (k − μ)2· P(X = k)
Alternativ kann die Varianz berechnet werden über die "Verschiebungsformel":
Var(X) = E(X2) - E(X)2
Var(X) = (Σ k2· P(X = k)) - μ2