Was ist eine normalverteilte Zufallsgröße X und wie bestimmt man die Wahrscheinlichkeit für Werte in einem Intervall [a; b]?
Eine Zufallsgröße X nennt man normalverteilt mit Erwartungswert μ und Standardabweichung σ, wenn ihre Dichtefunktion eine Gauß'sche Glockenfunktion φ mit den Parametern μ und σ ist.
Die Wahrscheinlichkeit, dass die Werte von X in einem Intervall [a; b] liegen, ist also das Integral über φ mit Untergrenze a und Obergrenze b, und kann mit dem Taschenrechner oder graphisch als Inhalt des entsprechenden Flächenstücks unter dem Graphen von φ ermittelt werden.
Beispiel 1
Die Zufallsgröße X ist normalverteilt mit
und
Ermittle die folgenden Wahrscheinlichkeiten auf drei Dezimalen genau. Verwende bei a) den Taschenrechner und ermittle die restlichen Wahrscheinlichkeiten ohne Taschenrechner, aber mit Begründung:
μ | = | 30 |
σ | = |
|
a)
P |
|
b)
P |
|
c)
P |
|
d)
P |
|
Zu a)
Je nach Taschenrechner-Modell findet man im Statistik-Menü eine Funktion namens "kumulierte Normalverteilung", "Normal-Dichte" o.ä. Je nach Modell kann man dort abgesehen von μ und σ die Ober- und die Untergrenze eines Intervalls eingeben oder nur eine Obergrenze. Im letzten Fall kann man also nur Wahrscheinlichkeiten der Form
unmittelbar bestimmen. Für Intervalle verwendet man die Umformung
So ermittelt man:
P |
|
| = |
|
| 0,904 |
Zu b)
Die Dichtefunktion einer normalverteilten Zufallsgröße X ist "symmetrisch bezüglich des Erwartungswerts" (genauer: bzgl. der senkrechten Geraden, die durch die Gleichung
ausgedrückt werden kann). Die Wahrscheinlichkeit, dass X im Intervall
liegt, ist genauso groß wie die Wahrscheinlichkeit, dass X im Intervall
liegt. Also gilt:
x | = | μ |
|
|
| = | 0,452 |
Zu c)
Einzelne Werte einer stetigen Zufallsgröße treten grundsätzlich mit Wahrscheinlichkeit 0 auf:
P |
|
Zu d)
Durch geschickte Zerlegung von ℝ, Ausnutzung der Symmetrie und Verwendung des Gegenereignisses ermittelt man:
| = |
| Zerlegung | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| = |
| Symmetrie | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| = |
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| = |
|
| ||||||||||||||||||||||||||||||||||||||||||||
| = |
| Gegenereignis | ||||||||||||||||||||||||||||||||||||||||||||
| = |
| |||||||||||||||||||||||||||||||||||||||||||||
| = |
| |||||||||||||||||||||||||||||||||||||||||||||
Beispiel 2
Ein Hersteller von Tiefkühl-Produkten stellt Apfelstrudel mit einem Nenngewicht von 600 Gramm her. Gemäß der sogenannten Fertigpackungsverordnung darf dieses um höchstens 15 Gramm unterschritten werden.
a) Ermittle die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter Apfelstrudel gegen die Verordnung verstößt, wenn die Gewichte der Apfelstrudel in Gramm normalverteilt sind, im Durchschnitt dem Nenngewicht entsprechen, jedoch eine Standardabweichung von 5 Gramm besitzen.
b) Bestimme außerdem die Wahrscheinlichkeit dafür, dass ein Apfelstrudel auf Gramm gerundet wirklich ein Gewicht von 600 Gramm besitzt.
X: Gewicht eines zufällig ausgewählten Apfelstrudels in Gramm
X ist normalverteilt mit
und
μ | = | 600 |
σ | = |
|
Zu a)
Ein Apfelstrudel verstößt gegen die Verordnung, wenn sein Gewicht um mehr als 15 Gramm das Nenngewicht unterschreitet, es also kleiner als 585 Gramm ist:
|
|
Anmerkung: Je nach Taschenrechner-Modell kann man diesen Wert nur durch Eingabe der Obergrenze 585 oder durch Eingabe von "unterer Grenze" -1000 (als Ersatz für -∞) und Obergrenze 585 ermitteln.
Zu b)
Damit ein Apfelstrudel auf Gramm gerundet 600 Gramm schwer ist, muss sein wirkliches Gewicht zwischen 599,5 und 600,5 Gramm liegen:
|
|
Anmerkung: Je nach Taschenrechner-Modell kann man diesen Wert durch Eingabe von "unterer Grenze" 599,5 und "oberer Grenze" 600,5 ermitteln oder aus der Differenz
, wenn jeweils nur eine Obergrenze eingegeben werden kann.
|
|
Beachte, dass ein "exaktes Gewicht" von 600 Gramm (ohne Rundung) jedoch mit 0% Wahrscheinlichkeit auftritt.

Lernvideo
Körpergröße
Kanal: Projekt MmF
Beispiel 3

Die Abbildung zeigt den Graphen der Dichtefunktion einer normalverteilten Zufallsgröße X.
a) Ermittle
P |
|
b) Bestimme u so, dass gilt:
|
|
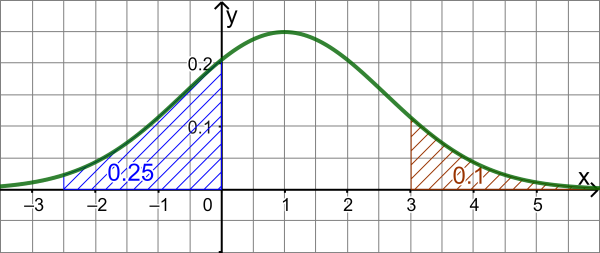
Zu a)
P |
|
x | = |
|
1. Methode: Abzählen der Kästchen ergibt etwa 10, wobei jedes Kästchen einer Wahrscheinlichkeit von
entspricht. Der gesuchte Wert ist somit ca.
| = | 0,025 |
| = |
|
2. Methode: Das Flächenstück entspricht ungefähr einem Dreieck mit Grundseite 2,5 und Höhe 0,2. Der gesuchte Wert ist also ungefähr
| = |
|
Zu b)
Der Inhalt der insgesamt zwischen Graph und x-Achse liegenden Fläche muss 1 betragen, aufgrund der Symmetrie des Graphen bezüglich der Geraden mit der Gleichung
gilt also
Im Intervall
liegen ca. 16 Kästchen zwischen Graph und x-Achse, was bereits einem Inhalt von
entspricht. Als "restlicher" Flächeninhalt bleibt also ungefähr übrig.
x | = | 1 |
| = |
|
|
| = | 0,4 |
0,1
Somit gilt
wenn man
wählt.
|
|
|

Lernvideo
Normalverteilung: Erwartungswert, Standardabweichung, Wahrscheinlichkeiten (So ähnlich im Abi)
Kanal: Mathehoch13
Siehe auch