Was versteht man unter einer Potenzfunktion und welche charakteristischen Eigenschaften und Spezialfälle hat sie?

Potenzfunktionen sind Funktionen der Form:
y = axn

Spezialfälle:
  • n = 0 (konstante Funktion): y = a, Graph: waagerechte Gerade
  • n = 1 (lineare Funktion): y = ax, Graph: Ursprungsgerade mit Steigung a
  • n = 2 (quadratische Funktion): y = ax2, Graph: gestauchte / gestreckte Parabel mit Scheitel S ( 0 | 0 )
Die Graphen von Potenzfunktionen haben charakteristische Eigenschaften, die oft davon abhängen, ob die Hochzahl n gerade oder ungerade ist.
  • Wertemenge:
    n gerade: keine negativen Zahlen
    n ungerade: alle reellen Zahlen

  • Symmetrie:
    n gerade: Achsensymmetrie zur y-Achse
    n ungerade: Punktsymmetrie zum Ursprung

  • Vorfaktor a
    Der Wert des Parameters a ist der Funktionswert an der Stelle x = 1.
    a>0: Streckung / Stauchung in y-Richtung
    a<0: zusätzliche Spiegelung an der x-Achse
Beispiel
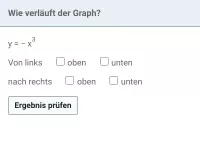
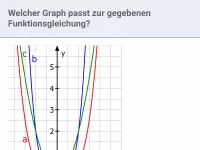
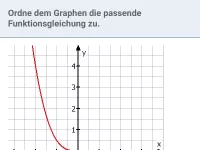
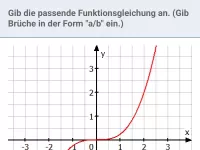
Gib die zugehörige Funktionsgleichung an
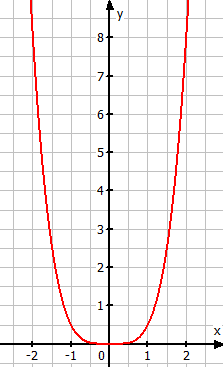
graphik
y
=
?x
?
Der Graph ist achsensymmetrisch zur y-Achse, also ist die Hochzahl gerade. Er verläuft von links oben nach rechts oben, also ist der Vorfaktor positiv.
Für x = 1 liest man ab:
y
=
0,5
Als mögliche Funktionsgleichung erhält man:
y
=
0,5x
n
 
n gerade
Möglich wären:
y
=
0,5x
2
y
=
0,5x
4
...
Um zu entscheiden, welche Funktionsgleichung die passende ist, setzt man einen weiteren x-Wert (z.B. x = 2) nacheinander in die Funktionsgleichungen ein und berechnet die zugehörigen y-Werte:
y
=
0,5
·
2
2
=
0,5
·
4
=
2
Der Punkt P ( 2 | 2 ) liegt nicht auf dem Graphen.
y
=
0,5
·
2
4
=
0,5
·
16
=
8
Der Punkt P ( 2 | 8 ) liegt auf dem Graphen, also stimmt die Funktionsgleichung:
y
=
0,5x
4
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen