Was sind stochastische Matrizen und wie werden sie verwendet?

Stochastische Matrizen

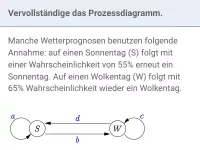
Stochastische Prozesse lassen sich sehr übersichtlich in Matrix-Schreibweise darstellen. Dazu werden die Zustandsverteilungen zu Vektoren zusammengefasst. Die Übergangswahrscheinlichkeiten finden sich in den Koeffizienten der Berechnungsvorschriften wieder und können übersichtlich in der Übergangsmatrix U dargestellt werden.

Die Zustandsverteilung nach Schritt k+1 kann mittels einer Matrix-Multiplikation aus der Übergangsmatrix U und der Zustandsverteilung nach Schritt k berechnet werden.

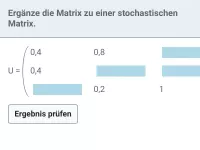
Eine Übergangsmatrix U zu einem vollständigen Prozessdiagramm nennt man auch stochastische Matrix und sie erfüllt folgende Eigenschaften:

  • U ist quadratisch (gleich viele Zeilen wie Spalten).
  • In der m-ten Spalte stehen die Übergangswahrscheinlichkeiten, mit denen man VOM m-ten Zustand aus die übrigen Zustände erreicht.
  • In der n-ten Zeile stehen die Übergangswahrscheinlichkeiten, mit denen man ZUM n-ten Zustand gelangt.
  • Summe der Spalteneinträge von U ist 1.

Werden im Prozessdiagramm NICHT ALLE möglichen Zustände berücksichtigt, so wird die Übergangsmatrix zum beschriebenen stochastischen Prozess auch keine stochastische Matrix sein.

Beispiel 1
Das folgende Prozessdiagramm beschreibt einen stochastischen Prozess:
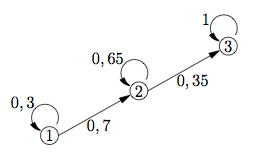
graphik
Stelle diesen Prozess mit Hilfe einer Übergangsmatrix dar.
Lösung:
  • Schritt 1: Prozessdiagramm in Gleichungen "übersetzen"
Die Zustandsverteilung nach k Schritten werde mit ak (Zustand 1), bk (Zustand 2) bzw. ck (Zustand 3) bezeichnet. Die Zustandsverteilung nach k+1 Schritten kann mit Hilfe des Prozessdiagramms berechnet werden.
Im folgenden Diagramm sind alle zum Zustand 1 führenden Wege grün, alle zum Zustand 2 führenden Wege blau und alle zum Zustand 3 führenden Wege rot gezeichnet:
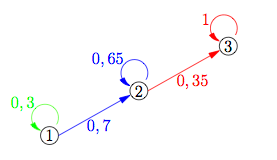
graphik
Damit ergibt sich für die Berechnung der Zustandsverteilung:
a
k
+
1
=
0,3
·
a
k
b
k
+
1
=
0,7
·
a
k
+
0,65
·
b
k
c
k
+
1
=
0,35
·
b
k
+
1
·
c
k
  • Schritt 2: Zustandsverteilung als Vektoren Schreiben
Die drei Gleichungen werden einfach als drei Zeilen eines Vektors geschrieben:
a
k
+
1
b
k
+
1
c
k
+
1
=
0,3
·
a
k
0,7
·
a
k
 
 
 
 
 
+
0,65
·
b
k
+
0,35
·
b
k
 
 
 
 
 
+
c
k
bzw.:
a
k
+
1
b
k
+
1
c
k
+
1
=
0,3
·
a
k
+
0
·
b
k
+
0
·
c
k
0,7
·
a
k
+
0,65
·
b
k
+
0
·
c
k
0
·
a
k
+
0,35
·
b
k
+
1
·
c
k
  • Schritt 3: Koeffizienten in der Übergangsmatrix auslagern
a
k
+
1
b
k
+
1
c
k
+
1
v
k
+
1
=
0,3
0,7
0
 
 
 
0
0,65
0,35
 
 
 
0
0
1
Übergangs
−
matrix U
·
a
k
b
k
c
k
v
k
Der im Prozessdiagramm dargestellte stochastische Prozess wird durch folgende Übergangsmatrix U beschrieben:
U
=
0,3
0,7
0
 
 
 
0
0,65
0,35
 
 
 
0
0
1
Bemerkung: Gäbe es zusätzlich auch noch Aufgaben auf einem vierten Schwierigkeitsniveau, welches 10% der Level 3-Schüler erreichen, könnte das Prozessdiagramm erweitert werden. Interessiert jedoch nur, wann wie viele Schüler im Level 3 angekommen sind, könnte das Prozessdiagramm auch unvollständig bleiben:
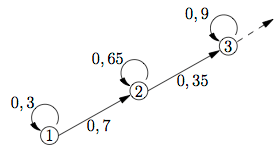
graphik
Die Übergangsmatrix sähe dann folgendermaßen aus und wäre insbesondere KEINE stochastische Matrix, da die letzte Spaltensumme NICHT 1 beträgt:
U
=
0,3
0,7
0
 
 
 
0
0,65
0,35
 
 
 
0
0
0,9
Beispiel 2
Ein stochastischer Prozess zwischen drei Zuständen ist durch folgende Übergangsmatrix gegeben:
U
=
0,3
0,7
0
 
 
 
0
0,65
0,35
 
 
 
0
0
1
v
k
 
sei die Zustandsverteilung nach k Schritten.
Startzustand: alle in Zustand 1
Bestimme die Zustandsverteilung nach 2 Schritten.
Lösung:
  • Bestimmung der Start-Zustandsverteilung:
Startzustand: alle in Zustand 1, daher:
v
0
=
1
0
0
  • Zustandsverteilung nach Schritt 1:
v
1
=
U
·
v
0
v
1
=
0,3
0,7
0
 
 
 
0
0,65
0,35
 
 
 
0
0
1
·
1
0
0
Das Ergebnis einer Multiplikation aus Matrix und Vektor ist wieder ein Vektor. Die Matrix wird dazu zeilenweise mit dem Spaltenvektor multipliziert.
v
1
=
0,3
·
1
+
0
·
0
+
0
·
0
0,7
·
1
+
0,65
·
0
+
0
·
0
0
·
1
+
0,35
·
0
+
1
·
0
v
1
=
0,3
0,7
0
  • Zustandsverteilung nach Schritt 2:
v
2
=
U
·
v
1
v
2
=
0,3
0,7
0
 
 
 
0
0,65
0,35
 
 
 
0
0
1
·
0,3
0,7
0
v
2
=
0,3
·
0,3
+
0
·
0,7
+
0
·
0
0,7
·
0,3
+
0,65
·
0,7
+
0
·
0
0
·
0,3
+
0,35
·
0,7
+
1
·
0
v
2
=
0,09
0,665
0,245
Beispiel 3
Ein stochastischer Prozess zwischen drei Zuständen A, B und C ist durch folgende Übergangsmatrix gegeben:
U
=
0,3
0,7
0
 
 
 
0,2
0,65
0,15
 
 
 
0
0
1
mit:
 
a
k
+
1
b
k
+
1
c
k
+
1
=
U
·
a
k
b
k
c
k
Interpretiere die Matrixeinträge in der Form:
? % BLEIBEN im Zustand ?.
bzw. ? % wechseln VON Zustand ? ZU Zustand ?
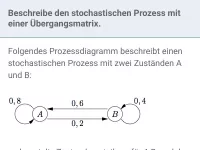
  • Interpretation der Diagonal-Einträge:
In der Diagonale der Matrix stehen genau die Anteile, die jeder Zustand bei sich hält, denn am Kreuzungspunkt m-te Spalte und m-te Zeile steht die Übergangswahrscheinlichkeit VON Zustand m ZU Zustand m:
U
=
0,3
0,7
0
 
 
 
 
0,2
0,65
0,15
 
 
 
 
 
0
0
1
Also:
30% von A BLEIBEN im Zustand A.
65% von B BLEIBEN im Zustand B.
100% von C BLEIBEN im Zustand C.
  • Interpretation der restlichen Einträge:
0,2 steht in der zweiten Spalte und ersten Zeile, also:
20% VON Zustand B wechseln ZU Zustand A.
0,7 steht in der ersten Spalte und zweiten Zeile, also:
70% VON Zustand A wechseln ZU Zustand B.
0,15 steht in der zweiten Spalte und dritten Zeile, also:
15% VON Zustand B wechseln ZU Zustand C.
Alle weiteren Matrixeinträge sind 0, daher betragen alle weiteren Übergangswahrscheinlichkeiten 0%.
Beispiel 4
Ein stochastischer Prozess zwischen drei Zuständen ist durch folgende Übergangsmatrix gegeben:
U
=
0,3
0,7
0
 
 
 
0
0,65
0,35
 
 
 
0
0
1
v
k
 
sei die Zustandsverteilung nach k Schritten.
Ist-Zustand: 15% in Zustand A, 48% in Zustand B, 37% in Zustand C
Bestimme die Zustandsverteilung einen Schritt vorher.
Lösung:
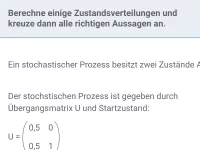
  • Bestimmung der gegebenen Zustandsverteilung:
Ist-Zustand, wir nennen ihn Zustand 1: 15% in Zustand A, 48% in Zustand B, 37% in Zustand C, daher:
v
1
=
0,15
0,48
0,37
  • Zusammenhang der gegebenen und gesuchten Zustandsverteilung:
Allgemein gilt:
v
k
+
1
=
U
·
v
k
Und daher:
v
1
=
U
·
v
0
 
 
 
 
 
 
 
 
 
 
bzw.:
 
 
 
U
·
v
0
=
v
1
v
1
 
ist gegeben, für
 
v
0
 
(Zustandsverteilung einen Schritt vorher) setzen wir Variablen ein. Das ergibt:
0,3
0,7
0
 
 
 
0
0,65
0,35
 
 
 
0
0
1
·
a
b
c
=
0,15
0,48
0,37
  • Aufstellen und Lösen des Gleichungssystems:
Die Multiplikation der Matrix mit dem Vektor liefert folgendes Gleichungssystem:
0,3a
0,7a
 
 
 
+
0,65b
+
0,35b
 
 
 
+
1c
 
=
=
=
 
0,15
0,48
0,37
 
Die erste Gleichung kann beidseitig durch 0,3 dividiert werden. Das liefert a = 0,5. Wird dies in die zweite Gleichung eingesetzt, erhält man:
a
0,7
·
0,5
 
 
 
+
0,65b
+
0,35b
 
 
 
+
1c
 
=
=
=
 
0,5
0,48
0,37
 
Jetzt kann die zweite Gleichung nach b aufgelöst werden (auf beiden Seiten 0,35 subtrahieren, anschließend durch 0,65 dividieren). Das Ergebnis b = 0,2 wird dann noch in die dritte Gleichung eingesetzt. Es ergibt sich:
a
 
 
 
 
b
0,35
·
0,2
 
 
 
+
1c
 
=
=
=
 
0,5
0,2
0,37
 
Die dritte Gleichung liefert c = 0,3:
a
 
 
 
 
b
 
 
 
 
c
 
=
=
=
 
0,5
0,2
0,3
 
Die Zustandsverteilung einen Schritt vorher war 50% in Zustand A, 20% in Zustand B und 30% in Zustand C.
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen