Wie berechnet man die Wahrscheinlichkeit eines Ereignisses E in einem mehrstufigen Zufallsexperiment?
Bei mehrstufigen Zufallsexperimenten kann ein Ereignis E mehrere Pfade im Baumdiagramm umfassen. Um die Wahrscheinlichkeit von E zu bestimmen, muss man die Wahrscheinlichkeiten dieser Pfade addieren (2. Pfadregel).
Beispiel
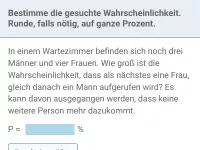
In einer Urne befinden sich zwei schwarze, zwei weiße und eine orange Kugeln. Es werden drei Kugeln hintereinander - ohne Zurücklegen - gezogen. Wie groß ist die Wahrscheinlichkeit, dass jede Farbe einmal drankommt?
Bei drei Farben und drei Ziehungen wird das gesamte Baumdiagramm sehr groß (bis zu
, darum beschränken wir uns hier auf die "gefragten" Pfade, bei denen alle drei Farben vorkommen:
| = | 27 Pfade) |
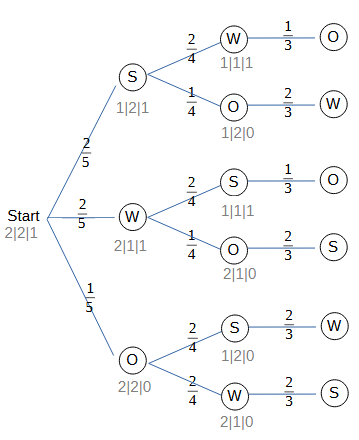
Nach der zweiten Pfadregel werden die Wahrscheinlichkeiten aller Pfade, die zum Ereignis "drei unterschiedliche Farben" gehören, addiert, d.h.
| = |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| = |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| = |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| = |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||