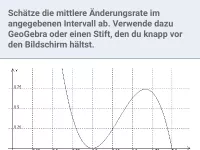
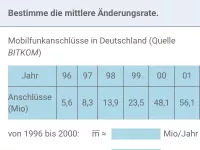
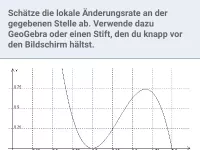
Wie ist der Zusammenhang zwischen dem Differenzenquotienten und der lokalen Änderungsrate?

Rechnerisch ergibt sich die lokale Änderungsrate an der Stelle x = a, indem man den Grenzwert des Differenzenquotienten

[ f(a+h) − f(a) ] / h

für h → 0 (h ≠ 0) bestimmt. Diesen Grenzwert (sofern er existiert) nennt man Differentialquotient.
Beispiel
Berechne die lokale Änderungsrate an der Stelle a.
f(x)
=
2
x
−
x
;
a
=
−
2
  • Differenzenquotient
f(-2+h)
−
f(-2)
h
=
2
−
2
+
h
−
−
2
+
h
−
2
−
2
−
−
2
h
=
2
−
2
+
h
+
2
−
h
+
1
−
2
h
=
2
h
−
2
+
1
−
h
h
=
- - - - - - - - - - - - - - - Erweitern:
2
h
−
2
+
h
−
2
h
−
2
−
h
·
h
−
2
h
−
2
h
=
2
+
h
−
2
−
h
·
h
−
2
h
−
2
h
=
h
−
h
2
+
2h
h
−
2
h
=
3h
−
h
2
h
−
2
h
=
3h
−
h
2
h
·
h
−
2
=
- - - - - - - - - - - - - - - im Zähler ausklammern:
h
·
3
−
h
h
·
h
−
2
- - - - - - - - - - - - - - - Kürzen:
3
−
h
h
−
2
  • Differentialquotient
Für h → 0 konvergiert der Differenzenquotient gegen
 
3
−
0
0
−
2
=
−
3
2
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen