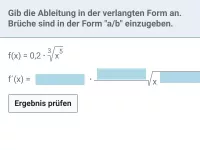
Wie lautet die Ableitung der Funktion f(x) = a · x^r?
Wenn f(x) = a · xr mit a ∈ ℝ und r ∈ ℚ \ {0}, dann ist
f ′(x) = a · r · x r−1.
f ′(x) = a · r · x r−1.
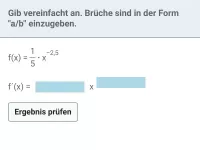
Beispiel 1
| = |
|
| = | ? |
Lösung:
| = |
| |||||||||||||||||||||||||||||||||||||||||||||||
|
| = |
| |||||||||||||||||||||||||||||||||||||||||||||||
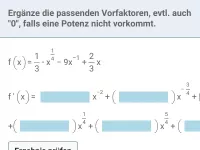
Beispiel 2
| = |
|
| = | ? |
- - - - - - - - - - - - - - - - Schreibe f (x) zunächst mit Hilfe von Potenzen:
| = |
|
- - - - - - - - - - - - - - - - Jetzt ableiten:
| = |
|
= |
|
- - - - - - - - - - - - - - - - Evtl. noch umformulieren:
= |
|

Lernvideo
Wurzelfunktion Produktregel Kettenregel
Kanal: Mathegym Basics
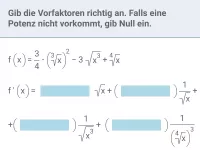
Beispiel 3
f(x) | = |
|
f´(x) | = | ? |
- Wandle zunächst in die Form a·xr um
f(x) | = |
|
- Ableitungsregel anwenden
| = |
| ||||||||||||||||||||
|
| = |
| ||||||||||||||||||||
|
| = |
| ||||||||||||||||||||