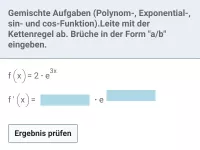
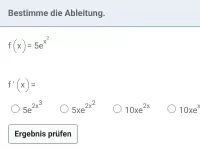
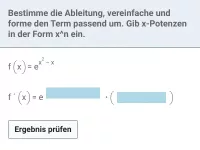
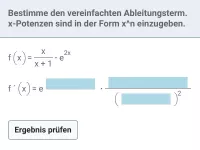
Wann und wie wird die Kettenregel in der Mathematik angewendet?

Kettenregel:

Wenn f(x) = g( h(x) ), dann ist f ′(x) = g′( h(x) )⋅h′(x)

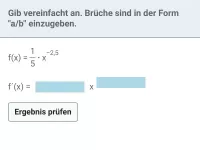
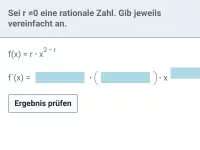
Beispiel 1
f
 
x
=
2x
2
−
8x
f ´
 
x
=
?
Anwendung der Kettenregel: die äußere Funktion 
…
 ergibt abgeleitet 
1
2
 
…
. Die innere Funktion 
2x
2
−
8x
 ist nachzudifferenzieren (markiert):
f
 
x
=
2x
2
−
8x
f ´
 
x
=
1
2
 
2x
2
−
8x
·
4x
−
8
4 ausklammern
f ´
 
x
=
1
2
 
2x
2
−
8x
·
4
 
x
−
2
mit 2 kürzen
=
2
 
x
−
2
2x
2
−
8x
Wurzelfunktion Produktregel Quotientenregel
Lernvideo

Wurzelfunktion Produktregel Quotientenregel

Kanal: Mathegym Basics
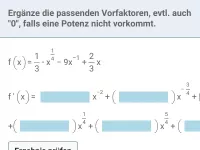
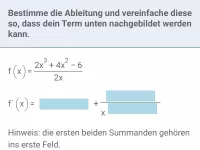
Beispiel 2
f
 
x
=
x
·
cos
e
x
f '
 
x
=
?
Es handelt sich um ein Produkt (⇒Produktregel). Der zweite Faktor ist eine Verkettung (⇒Kettenregel).
- - - - - - - - - - - - Vorbereitend:
x
 
abgeleitet:   
 
1
cos
e
x
 
abgeleitet:   
 
−
sin
e
x
·
e
x
 
Kettenregel
- - - - - - - - - - - - Produktregel:
f '
 
x
=
1
·
cos
e
x
+
x
·
−
sin
e
x
·
e
x
        
 
=
cos
e
x
−
x
·
e
x
·
sin
e
x
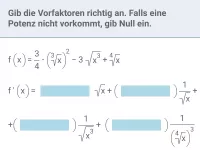
Beispiel 3
f
 
x
=
1
−
3x
·
sin
x
f '
 
x
=
?
Es handelt sich um ein Produkt (⇒Produktregel). Der erste Faktor ist eine Verkettung (⇒Kettenregel).
- - - - - - - - - - - - Vorbereitend:
1
−
3x
 
abgeleitet:   
 
1
2
 
1
−
3x
·
−
3
 
Kettenregel
sin
x
 
abgeleitet:   
 
cos
x
- - - - - - - - - - - - Produktregel:
f '
 
x
=
1
2
 
1
−
3x
·
−
3
·
sin
x
+
1
−
3x
·
cos
x
        
 
=
−
3
 
sin
x
2
 
1
−
3x
+
1
−
3x
·
cos
x
Wurzelfunktion Produktregel Quotientenregel
Lernvideo

Wurzelfunktion Produktregel Quotientenregel

Kanal: Mathegym Basics
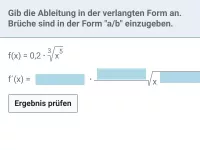
Beispiel 4
f
 
x
=
x
·
cos
ln(x)
f '
 
x
=
?
Es handelt sich um ein Produkt (⇒Produktregel). Der zweite Faktor ist eine Verkettung (⇒Kettenregel).
- - - - - - - - - - - - Vorbereitend:
x
 
abgeleitet:   
 
1
cos
ln(x)
 
abgeleitet:   
 
−
sin
ln(x)
·
1
x
 
Kettenregel
- - - - - - - - - - - - Produktregel:
f '
 
x
=
1
·
cos
ln(x)
+
x
·
−
sin
ln(x)
·
1
x
        
 
=
cos
ln(x)
−
sin
ln(x)
ln(x) Produktregel Kettenregel
Lernvideo

ln(x) Produktregel Kettenregel

Kanal: Mathegym Basics
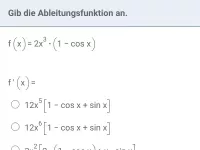
Beispiel 5
Bestimme die Ableitung.
f
 
x
=
1
3
·
sin
x
3
−
3x
+
2
Anwendung der Kettenregel: die äußere Funktion "sin(…)" ergibt abgeleitet "cos(…)", die innere Funktion 
x
3
−
3x
+
2
 wird nachdifferenziert (markiert):
f ´
 
x
=
1
3
·
cos
x
3
−
3x
+
2
·
3x
2
−
3
3 ausklammern
f ´
 
x
=
1
3
·
cos
x
3
−
3x
+
2
·
3
 
x
2
−
1
zusammenfassen
=
x
2
−
1
·
cos
x
3
−
3x
+
2
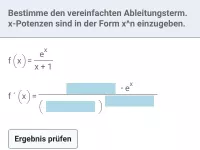
Beispiel 6
f
 
x
=
cos
2
x
3x
f ´
 
x
=
?
Für die Anwendung der Quotientenregel bereitet man die Ableitung der Zählerfunktion vor:
z
x
=
cos
2
x
z ´
 
x
=
2cos
x
·
−
sin
x
=
−
2cos
x
·
sin
x
Jetzt lässt sich die Quotientenregel leichter anwenden:
f ´
 
x
=
z ´
 
x
·
3x
−
z
x
·
3
3x
2
=
−
2cos
x
·
sin
x
·
3x
−
cos
2
x
·
3
9x
2
−
3cos
x
 
ausklammern
=
−
3cos
x
9x
2
·
2x
·
sin
x
+
cos
x
mit 3 kürzen
=
−
cos
x
3x
2
·
2x
·
sin
x
+
cos
x
Quotientenregel Kettenregel e^x sin(x)
Lernvideo

Quotientenregel Kettenregel e^x sin(x)

Kanal: Mathegym Basics
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen