Exp, Mathe-Aufgaben
Exp, Aufgaben und Online-Übungen inkl. Lösung, Erklär-Videos und Hilfestellungen.
Auf unserer mehrfach prämierten Mathe-Lernplattform, die auch an 588 Schulen verwendet wird.
Viele unterschiedliche Mathe-Aufgaben und Mathe-Übungen zu 291 Themen der Schulmathematik.

-
≈Oberstufe - Aufgaben + Stoff + Video
exp und ln - Ableitung
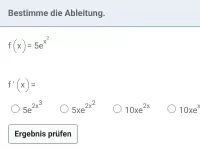
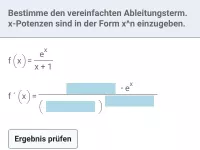
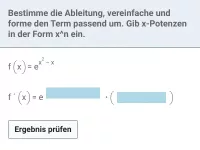
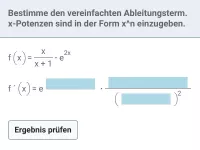
Ableitungsregeln für exp und ln (natürliche Exponentialfunktion/natürliche Logarithmusfunktion), Produkte, Quotienten und Verkettungen von exp und ln mit anderen Funktionen und deren Ableitungen -
≈Oberstufe - Aufgaben + Stoff + Video
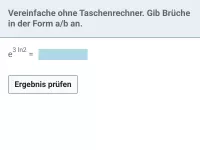
exp und ln - Gleichungen lösen
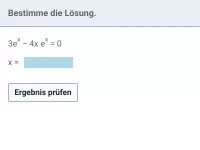
Gleichungen lösen, die sich auf e^f(x)=b bzw. ln(...)=b zurückführen lassen -
≈Oberstufe - Aufgaben + Stoff + Video
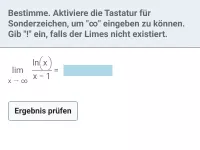
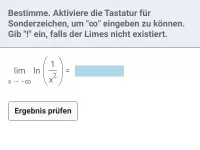
exp und ln - Grenzwertbetrachtungen
Verhalten für x → ∞ und für x → x0 bei Funktionen, die sich u.a. aus exp oder ln zusammensetzen -
≈Oberstufe - Aufgaben + Stoff + Video
exp und ln - Verschiebung, Streckung und Spiegelung
Spiegelung des Graphen an der x- und y-Achse, Verschiebung in x- und y-Richtung, Streckung und Stauchung -
≈Oberstufe - Aufgaben + Stoff + Video
Funktionsuntersuchung - exp und ln
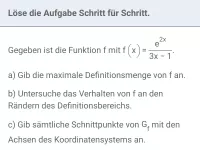
Funktionen und Funktionsscharen, die exp oder ln enthalten, hinsichtlich Dmax, Nullstellen, Verhalten im Unendlichen, Symmetrie des Graphen zum KOSY, relativen Hoch- und Tiefpunkten und weiterer Aspekte untersuchen. -
≈Oberstufe - Aufgaben + Stoff
Modellieren von Wachstums- und Abklingvorgängen
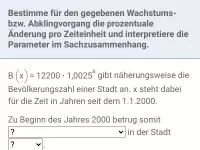
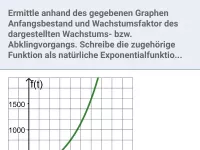
Beschreibung von Wachstums- und Abklingvorgängen mit Hilfe der natürlichen Exponentialfunktion; u.a. Ermittlung des Wachstumsfaktors, der Wachstumsgeschwindigkeit, Verdoppelungs- und Halbwertszeit; Basiswechsel von b zu e -
≈9. Klasse - Aufgaben + Stoff + Video
Quadratische Funktionen - einführende Aufgaben mit a≠1
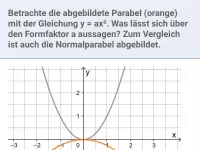
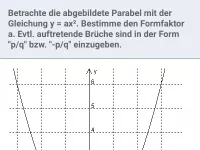
Gestreckte und gestauchte Parabeln, Bestimmung von Parametern (insbesondere Formparameter) anhand des Grafen, leichte Scheitelbestimmung
Fragen und Antworten zum Thema "exp"
- Was lässt sich über die Graphen der Funktionen folgender Gleichungen jeweils aussagen: y = x², y = (x + 2)², y = x² + 2, y = (x - 1)² + 3?
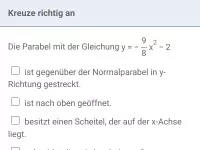
- Was sagt der Graph der Funktion y = ax² (a≠0) über die Form der Parabel aus?
- Wie bestimmt man den Formparameter a einer Parabel, wenn die Gleichung bis auf diesen bekannt ist?
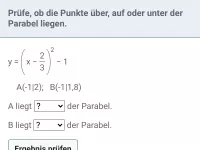
- Wie überprüft man, ob ein Punkt bezüglich eines Funktionsgraphen auf, über oder unter diesem liegt?
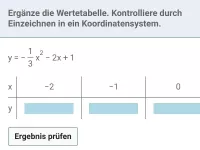
- Wie erstellt man eine Wertetabelle für eine Funktion und was bedeuten die Einträge?
- Wann und wie wird die Kettenregel in der Mathematik angewendet?
- Was besagt die Produktregel in der Differentialrechnung?
- Was besagt die Quotientenregel in der Differentialrechnung?
- Wie kann eine Funktion f(x) abgewandelt werden, um ihren Graphen Gf zu strecken, stauchen, verschieben oder zu spiegeln?
- Wie lauten die Ableitungen der Exponentialfunktion und der natürlichen Logarithmusfunktion?
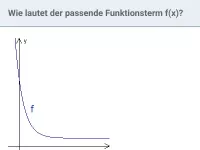
- Wie verhält sich die Exponentialfunktion exp(x) für x gegen plus oder minus unendlich?
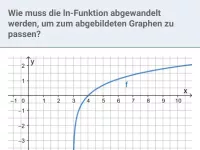
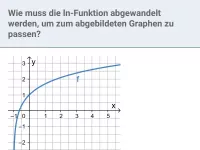
- Wie verhält sich die natürliche Logarithmusfunktion ln(x) an den Rändern ihres Definitionsbereichs?
- Wie verhalten sich die Funktionen x^n und e^x für x → ∞ und x → −∞?
- Wie verhalten sich der Quotient aus ln(x) und x^n für x → ∞ und das Produkt aus ln(x) und x^n für x → 0^+?
- Wie lauten die Produkt- und Quotientenregel der Ableitung?
- Wie bewirkt man durch Änderung des Funktionsterms eine Spiegelung an der x-Achse oder y-Achse sowie eine Verschiebung in y-Richtung?
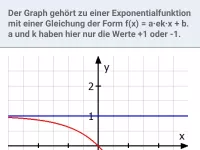
- Wie lautet die Gleichung der Asymptote bei Exponentialfunktionen vom Typ f(x) = a e^(kx) + b?
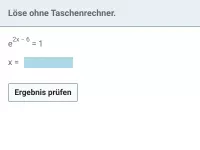
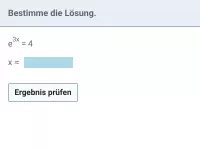
- Wie löst man Exponentialgleichungen der Form e^{f(x)} = b?
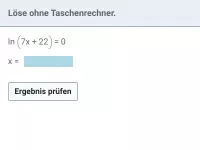
- Wie löst man Gleichungen der Form ln(...) = b und was ergibt sich, wenn b = 0?
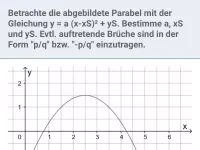
- Wie beeinflussen die Parameter a, xS und yS die Form und Lage einer Parabel mit der Gleichung y = a⋅(x - xS)² + yS?
- Wie zeichnet man eine Parabel in Scheitelform ohne Wertetabelle?
- Was ist die Ableitung der natürlichen Exponentialfunktion?
- Wie sind die Funktionen e^x und ln(x) miteinander verbunden?
- Wie lautet der Funktionsterm für exponentielles Wachstum und Abklingen und wie bestimmt man die Parameter und die prozentuale Änderung?
- Wie kann man den Funktionsterm eines Wachstums- oder Abklingvorgangs zwischen beliebiger Basis und natürlicher Exponentialfunktion umwandeln?
- Was sind Verdopplungszeit und Halbwertszeit und wie berechnet man sie aus einem Funktionsterm?