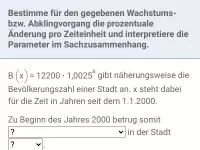
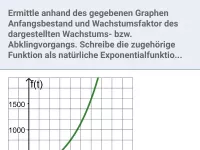
Wie kann man den Funktionsterm eines Wachstums- oder Abklingvorgangs zwischen beliebiger Basis und natürlicher Exponentialfunktion umwandeln?

Beim Modellieren von Wachstums- und Abklingvorgängen benötigt man statt Exponentialfunktionen mit beliebiger Basis oft natürliche Exponentialfunktionen, z.B. wenn die Ableitung gesucht ist. Dazu ersetzt man die bisherige Basis a durch den äquivalenten Term eln(a) und schreibt f(t)=b⋅eln(a)⋅t. Umgekehrt kann man statt ek⋅t einfach (ek)t schreiben, so dass ek dem Wachstumsfaktor entspricht.
Beispiel 1
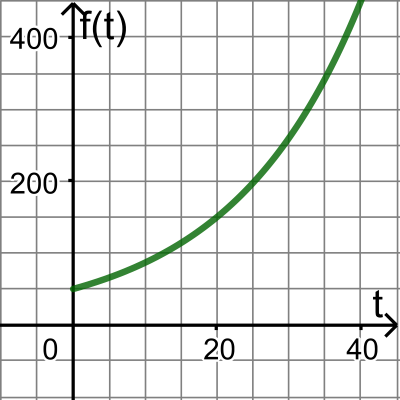
graphik
Die Abbildung zeigt den Graphen eines exponentiellen Wachstumsvorgangs. Bestimme einen passenden Term und verwende dabei die natürliche Exponentialfunktion.
  • 1. Lösungsmöglichkeit
Der Anfangsbestand ist der y-Achsenabschnitt, also 50.
Da sich der Bestand jeweils in zwanzig Zeiteinheiten verdreifacht, ist der Wachstumsfaktor (pro Zeiteinheit!) 
20
3
 
≈
 
1,056.
(Begründung: Wenn pro Zeiteinheit der Wachstumsfaktor a beträgt, muss die betrachtete Größe sich nach 20 Zeiteinheiten mit dem Faktor 
a
20
 verändert haben. Aus 
a
20
=
3
 folgt das obige Ergebnis.)
Umformung in eine natürliche Exponentialfunktion:
f
 
t
=
50
·
20
3
t
=
50
·
e
ln
 
20
3
·
t
 
≈
 
50
·
e
0,055t
  • 2. Lösungsmöglichkeit
Man liest die Punkte 
0
 
|
 
50
 und 
20
 
|
 
150
 vom Graphen ab und geht vom Ansatz 
f
 
t
=
b
·
e
k
·
t
 aus. Es ergibt sich das Gleichungssystem
 
I.
    
    
b
·
e
k
·
0
=
50
II.
    
 
b
·
e
k
·
20
=
150
 
I'.
 
    
    
b
=
50
I'. in II.
 
50
·
e
20k
=
150
:
50
e
20k
=
3
ln
 
…
20k
=
ln
 
3
:
20
k
=
ln
 
3
:
20
=
−
0,0549…
Mit sinnvoll gerundeten Werten ergibt sich 
f
 
t
 
≈
 
50
·
e
0,055
·
t
 
.
Beispiel 2
Ein Patient erhält nach einer Operation eine Infusion mit Schmerzmittel. Näherungsweise soll angenommen werden, dass die Menge des Wirkstoffs im Blut des Patienten nach der Infusion exponentiell abnimmt. Zu Beginn sind 800mg des Wirkstoffs im Blut enthalten, nach drei Stunden hat sich die Wirkstoffmenge durch Verstoffwechslung in der Leber halbiert. Ermittle die Änderungsrate der Wirkstoffmenge im Blut nach einer Stunde. Gib zudem die Einheit und die Bedeutung dieses Werts im Sachzusammenhang an.
  • Aufstellen eines geeigneten Funktionsterms
Der Anfangsbestand 800(mg) ist gegeben. t steht für die Zeit in Stunden, die seit der Infusion vergangen ist.
Mit dem Ansatz 
f
 
t
=
800
·
e
k
·
t
 und dem Wertepaar 
 
3
 
|
 
400
 
 ermittelt man k wie folgt:
f(3)
=
400
800
·
e
k
·
3
=
400
:
800
e
3k
=
0,5
ln
 
…
3k
=
ln
 
0,5
:
3
k
=
ln
 
0,5
3
Also 
k
 
≈
 
−
0,231
  • Ermittlung der Ableitung
Unter Beachtung der Kettenregel gilt:
f
 
t
=
800
·
e
−
0,231t
f
 
'
 
t
=
800
·
e
−
0,231t
·
−
0,231
=
−
184,8
·
e
−
0,231t
  • Bestimmung der gesuchten "Wachstums"geschwindigkeit
Nach 1 Stunde erhält man:
f
 
'
 
1
=
−
184,8
·
e
−
0,231
·
1
 
≈
 
−
147
  • Interpretation dieses Werts
Die Wirkstoffmenge nimmt nach einer Stunde mit einer Änderungsrate von 
−
147
 
mg
h
 (Milligramm pro Stunde) ab.
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen