Wie lautet der Funktionsterm für exponentielles Wachstum und Abklingen und wie bestimmt man die Parameter und die prozentuale Änderung?

Mithilfe eines Funktionsterms der Form f(t)=b⋅a^t kann man exponentielle Wachstums- und Abklingvorgänge modellieren. Dabei steht t für die Zeit (in einer bestimmten Zeiteinheit), b = f(0) für den Anfangsbestand und a für den Wachstumsfaktor.

Aus dem Wachstumsfaktor kann man die prozentuale Änderungsrate pro Zeiteinheit ermitteln, indem man (a-1)⋅100% rechnet, indem man also vom Wachstumsfaktor 1 subtrahiert und das Ergebnis in Prozent schreibt.

Beispiel

25000

1,025

gibt näherungsweise die Bevölkerungsentwicklung einer Stadt an. t steht für die Zeit in Jahren seit 2000. Interpretiere die Werte 25000 und 1,025 im Sachzusammenhang und gib an, wie sich die Bevölkerungszahl der Stadt prozentual pro Jahr verändert.

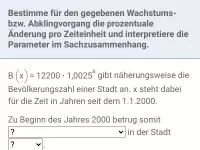
25000 ist der Anfangsbestand, also die Bevölkerungszahl im Jahr 2000.

1,025 ist der Wachstumsfaktor.

Somit nimmt die Bevölkerungszahl der Stadt pro Jahr um

1,025

−

0,025

2,5%

zu.

Siehe auch