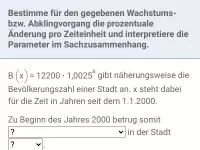
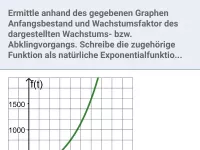
Was sind Verdopplungszeit und Halbwertszeit und wie berechnet man sie aus einem Funktionsterm?
Für einen exponentiellen Wachstumsvorgang mit dem Funktionsterm f(t) gibt es stets eine Zeitspanne TV (Verdopplungszeit), in der sich die betrachtete Größe verdoppelt. Man ermittelt sie durch Auflösen der Gleichung f(TV) = 2 ⋅ f(0).
Entsprechend gibt es für einen exponentiellen Abklingvorgang mit dem Funktionsterm f(t) stets eine Zeitspanne TH (Halbwertszeit), in der sich die betrachtete Größe halbiert. Man erhält sie durch Auflösen der Gleichung f(TH) = 0,5 ⋅ f(0).
Beispiel
Eine Messgröße kann mithilfe des Terms
modelliert werden. Dabei steht
für die Zeit in Minuten. Begründe, ob es eine Zeitspanne gibt, in der sich die Messgröße jeweils verdoppelt oder halbiert, und berechne diese Zeitspanne gegebenenfalls.
f(t) | = |
|
| 0 |
Da der Exponent negativ ist, handelt es sich um eine abnehmende Exponentialfunktion. Es gibt also eine zugehörige Halbwertszeit
, die man wegen
wie folgt berechnen kann:
T | H |
f(0) | = | 18 |
| = |
|
| ||||||||||||||||||||||
| = |
|
| ||||||||||||||||||||||
| = |
|
| ||||||||||||||||||||||
| = |
|
| ||||||||||||||||||||||
Somit halbiert sich die Messgröße jeweils innerhalb einer Zeitspanne von ca. 10,7 Minuten.