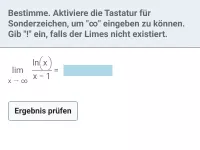
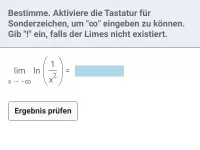
Wie verhält sich die natürliche Logarithmusfunktion ln(x) an den Rändern ihres Definitionsbereichs?
ln(x) strebt
- gegen −∞ für x → 0+
- gegen ∞ für x → ∞
Beispiel
| = | ? |
Zunächst betrachtet man nur die Entwicklung des Arguments der ln-Funktion.
| = | ∞ |
Erläuterung: es handelt sich um eine gebrochen-rationale Funktion, wobei der Zählergrad größer als der Nennergrad ist. Eine solche Funktion wächst für
IMMER gegen ∞ oder −∞. Um das richtige Vorzeichen herauszufinden, berachten wir Zähler und Nenner für sehr kleine x-Werte (z.B. -1000) getrennt: im Zähler wird von 1 eine große positive Zahl abgezogen (positiv, das quadratisch), also ist der Zähler negativ. Der Nenner ist ebenfalls negativ. Nach der Regel "Minus:Minus=Plus" kommt man also auf +∞.
| ∞ |
Jetzt ist klar, wie sich der Gesamtterm entwickelt:
| = | ∞ |

Lernvideo
Limes einer zusammengesetzten Funktion für x gegen Unendlich, Beispiel
Kanal: Mathegym