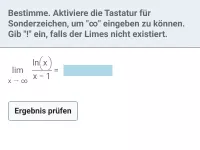
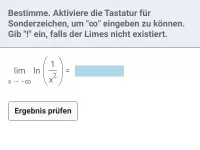
Wie verhalten sich die Funktionen x^n und e^x für x → ∞ und x → −∞?
Die natürliche Exponentialfunktion verändert sich wesentlich schneller als jede Potenzfunktion. Daher gilt:
- für x → −∞ strebt das Produkt aus ex und xn gegen 0
- für x → ∞ strebt der Quotient aus xn und ex gegen 0
- für x → ∞ strebt die Differenz aus ex und xn gegen ∞
Beispiel
| = | ? |
Entwicklung des ersten Faktors:
| = | ∞ |
Entwicklung des zweiten Faktors:
| = | 0 |
Erläuterung: ist der Zählergrad einer gebrochen rationalen Funktion kleiner als der Nennergrad, so geht der Funktionswert für
IMMER gegen 0.
| ∞ |
Entwicklung des Gesamtterms:
Wenn in einem Produkt der eine Faktor gegen ∞ und der andere gegen 0 geht, kann man ohne weitere Betrachtung KEINE Aussage darüber machen, wie sich der Term insgesamt entwickelt (das Argument "0 mal … ist 0" greift hier nicht, da ∞ keine Zahl ist). Weitere Betrachtung: der erste Faktor wächst exponentiell gegen ∞, daher ist dieser Faktor gegenüber dem zweiten dominant, d.h.
| = | ∞ |

Lernvideo
Limes einer zusammengesetzten Funktion für x gegen Unendlich, Beispiel
Kanal: Mathegym