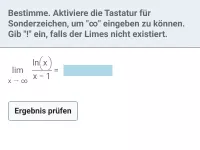
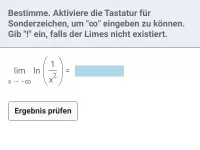
Wie verhalten sich der Quotient aus ln(x) und x^n für x → ∞ und das Produkt aus ln(x) und x^n für x → 0^+?
Die ln-Funktion verändert sich wesentlich langsamer als jede Potenzfunktion. Daher gilt:
- für x → ∞ strebt der Quotient aus ln(x) und xn gegen 0
- für x → 0+ strebt das Produkt aus ln(x) und xn gegen 0
Beispiel
| = | ? |
Entwicklung des Zählers:
| = |
|
Entwicklung des Nenners:
| = |
|
Entwicklung des Gesamtterms:
Wenn in einem Bruchterm Zähler und Nenner jeweils gegen ∞ oder 0 gehen, kann man ohne weitere Betrachtung KEINE Aussage darüber machen, wie sich der Term insgesamt entwickelt. Weitere Betrachtung: da der ln langsamer wächst als jeder Potenzfunktion, setzt sich hier der Nenner durch, d.h.
| = | 0 |

Lernvideo
Limes einer zusammengesetzten Funktion für x gegen Unendlich, Beispiel
Kanal: Mathegym