Wie überprüft man, ob ein Punkt bezüglich eines Funktionsgraphen auf, über oder unter diesem liegt?
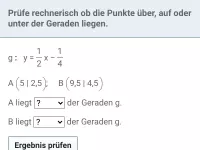
Um zu überprüfen, ob ein Punkt (a|b) über, auf oder unter dem Graphen einer Funktion liegt, setzt man a in den Funktionsterm f(x) ein. Der Punkt liegt
- über dem Graphen, wenn b > f(a)
- auf dem Graphen, wenn b = f(a)
- unter dem Graphen, wenn b < f(a)
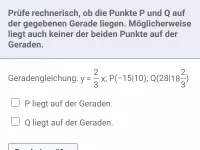
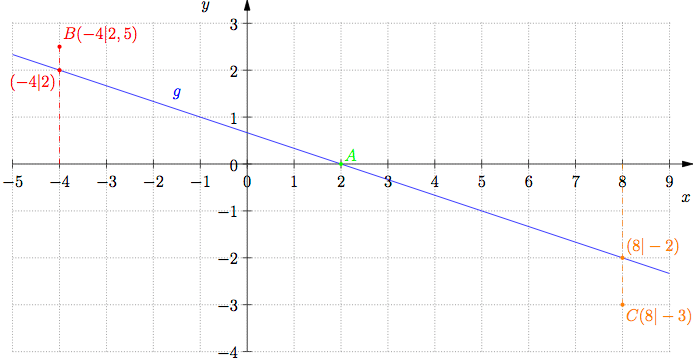
Beispiel 1
g:
;
;
;
y | = |
|
A |
|
B |
|
C |
|
Gib jeweils an, ob der der Punkt über, auf oder unter der Geraden liegt.
- Lage von Punkt A
Punkt A hat die x-Koordinate 2. Berechne daher den Funktionswert der Geraden g an der Stelle 2:
| = |
| |||||||||||||||||||||
|
| = |
| |||||||||||||||||||||
|
| = |
| |||||||||||||||||||||
Also liegt der Punkt
auf der Geraden.
A |
|
- Lage von Punkt B
Punkt B hat die x-Koordinate −4. Berechne daher den Funktionswert der Geraden g an der Stelle −4:
| = |
| ||||||||||||||||||||||||||||
|
| = |
| ||||||||||||||||||||||||||||
|
| = |
| ||||||||||||||||||||||||||||
|
| = |
| ||||||||||||||||||||||||||||
Also liegt der Punkt
auf der Geraden. Der Punkt
liegt dagegen oberhalb der Geraden, da die y-Koordinate größer ist:
|
B |
|
| 2 |
- Lage von Punkt C
Punkt C hat die x-Koordinate 8. Berechne daher den Funktionswert der Geraden g an der Stelle 8:
| = |
| |||||||||||||||||||||
|
| = |
| |||||||||||||||||||||
|
| = |
| |||||||||||||||||||||
|
| = |
| |||||||||||||||||||||
Also liegt der Punkt
auf der Geraden. Der Punkt
liegt dagegen unterhalb der Geraden, da die y-Koordinate kleiner ist:
.
|
C |
|
| −2 |
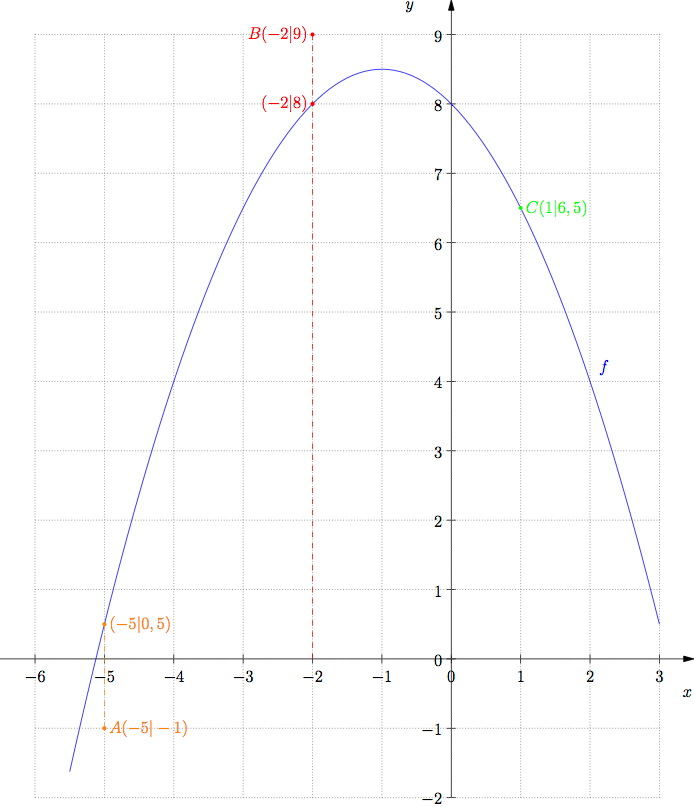
Beispiel 2
f:
;
;
;
y | = |
|
A |
|
B |
|
C |
|
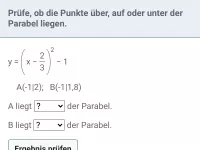
Gib jeweils an, ob der der Punkt über, auf oder unter der Parabel liegt.
- Lage von Punkt A
Punkt A hat die x-Koordinate −5. Berechne daher den Funktionswert der Parabel f an der Stelle −5:
| = |
| ||||||||||||||||||||||||||||||||||||
|
| = |
| ||||||||||||||||||||||||||||||||||||
|
| = |
| ||||||||||||||||||||||||||||||||||||
Also liegt der Punkt
auf der Parabel. Der Punkt
liegt dagegen unterhalb der Parabel, da die y-Koordinate kleiner ist:
.
|
A |
|
| 0,5 |
- Lage von Punkt B
Punkt B hat die x-Koordinate −2. Berechne daher den Funktionswert der Parabel f an der Stelle −2:
| = |
| ||||||||||||||||||||||||||||||||||||
|
| = |
| ||||||||||||||||||||||||||||||||||||
|
| = |
| ||||||||||||||||||||||||||||||||||||
Also liegt der Punkt
auf der Parabel. Der Punkt
liegt dagegen oberhalb der Parabel, da die y-Koordinate größer ist:
|
B |
|
| 8 |
- Lage von Punkt C
Punkt C hat die x-Koordinate 1. Berechne daher den Funktionswert der Parabel f an der Stelle 1:
| = |
| ||||||||||||||||||||||||
|
| = |
| ||||||||||||||||||||||||
|
| = |
| ||||||||||||||||||||||||
Also liegt der Punkt
auf der Parabel.
C |
|
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
-
≈8. Klasse - Aufgaben + Stoff + Video
Lineare Funktionen - Lage Punkt/Gerade rechnerisch
Überprüfung, ob Punkt auf, unter- oder oberhalb einer Geraden mit gegebenem Term liegt. -
≈9. Klasse - Aufgaben + Stoff + Video
Quadratische Funktionen - einführende Aufgaben mit a≠1
Gestreckte und gestauchte Parabeln, Bestimmung von Parametern (insbesondere Formparameter) anhand des Grafen, leichte Scheitelbestimmung
Ähnliche Themen
- Was lässt sich über die Graphen der Funktionen folgender Gleichungen jeweils aussagen: y = x², y = (x + 2)², y = x² + 2, y = (x - 1)² + 3?
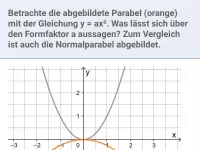
- Was sagt der Graph der Funktion y = ax² (a≠0) über die Form der Parabel aus?
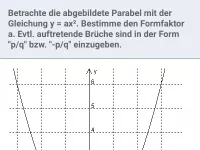
- Wie bestimmt man den Formparameter a einer Parabel, wenn die Gleichung bis auf diesen bekannt ist?
- Wie erstellt man eine Wertetabelle für eine Funktion und was bedeuten die Einträge?
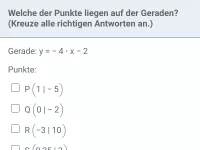
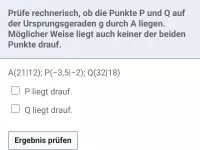
- Wie kann man rechnerisch überprüfen, ob ein Punkt auf einer Geraden liegt?
- Wie berechnet man die fehlende Koordinate eines Punktes auf einer Geraden, wenn eine Koordinate bekannt ist?
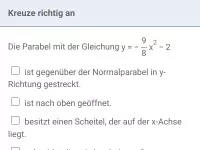
- Wie beeinflussen die Parameter a, xS und yS die Form und Lage einer Parabel mit der Gleichung y = a⋅(x - xS)² + yS?
- Wie zeichnet man eine Parabel in Scheitelform ohne Wertetabelle?