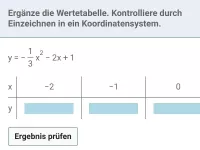
Wie beeinflussen die Parameter a, xS und yS die Form und Lage einer Parabel mit der Gleichung y = a⋅(x - xS)² + yS?
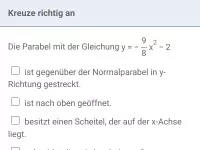
Durch die Gleichung y = a⋅(x - xS)² + yS (a≠0) ist eine Parabel mit den Scheitelkoordinaten xS und yS gegeben, die gegenüber der Normalparabel mit der Gleichung y = x²
- nach unten geöffnet ist, falls a negativ ist und
- evtl. gestreckt (falls |a|>1) bzw. gestaucht (falls |a|<1) ist.
Beispiel
Abgebildet ist die Parabel mit der Gleichung
y | = |
|
Bestimme a,
und
.
x | S |
y | S |
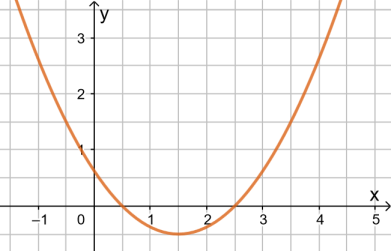
- Scheitel ablesen ⇒ xS und yS
Aufgrund des Scheitelpunkts S(1,5|-0,5) können
und
direkt angegeben werden. Damit lautet die die Gleichung
| = |
|
| = |
|
y | = |
|
- Weiteren Punkt ablesen ⇒ a
Lies z.B. den Punkt P(2,5|0) ab und setze ihn in die Gleichung ein. Dann löse nach a auf:
| = |
| |||||||||||||||||
| = |
|
| ||||||||||||||||
| = |
| |||||||||||||||||
Weitere Beispiele im nachfolgenden Video.

Lernvideo
Funktionsgleichung bestimmen PARABEL – Quadratische Funktionen ablesen
Kanal: MathemaTrick
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
- Was lässt sich über die Graphen der Funktionen folgender Gleichungen jeweils aussagen: y = x², y = (x + 2)², y = x² + 2, y = (x - 1)² + 3?
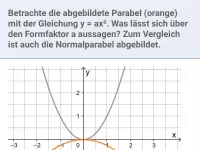
- Was sagt der Graph der Funktion y = ax² (a≠0) über die Form der Parabel aus?
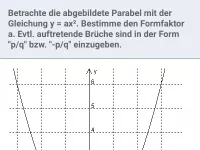
- Wie bestimmt man den Formparameter a einer Parabel, wenn die Gleichung bis auf diesen bekannt ist?
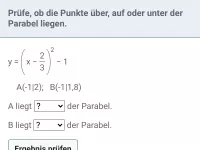
- Wie überprüft man, ob ein Punkt bezüglich eines Funktionsgraphen auf, über oder unter diesem liegt?
- Wie erstellt man eine Wertetabelle für eine Funktion und was bedeuten die Einträge?
- Wie zeichnet man eine Parabel in Scheitelform ohne Wertetabelle?