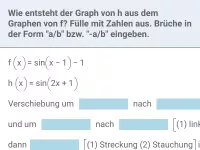
Wie kann eine Funktion f(x) abgewandelt werden, um ihren Graphen Gf zu strecken, stauchen, verschieben oder zu spiegeln?
| h ( x ) = | Gh geht aus Gf hervor durch |
| f ( x + a ) | Verschiebung um |a| Einheiten nach rechts (a < 0) bzw. links (a > 0) |
| f ( x ) + a | Verschiebung um |a| Einheiten nach oben (a > 0) bzw. unten (a < 0) |
| a · f ( x ), a > 0 | Streckung (a > 1) bzw. Stauchung (a < 1) in y-Richtung |
| − f ( x ) | Spiegelung an der x-Achse |
| f ( a · x ), a > 0 | Streckung mit Faktor 1/a in x-Richtung |
| f ( −x ) | Spiegelung an der y-Achse |
Beispiel 1
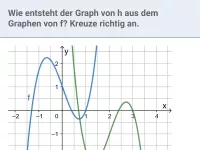
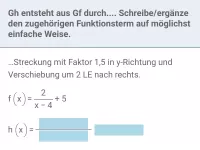
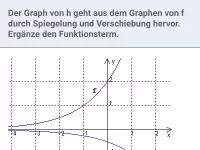
Wie entsteht der Graph von h aus dem Graphen von f? Gib einen passenden Term für h an.
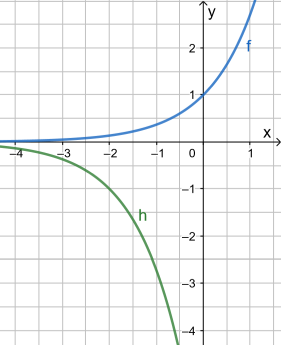
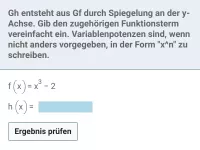
Lösung: Wie man unten sieht, erhält man den Graphen von h, indem man den Graphen von f zunächst an der x-Achse spiegelt (setze also ein "Minus" vor den Funktionsterm) und anschließend um 2 Einheiten nach links verschiebt (ersetze x durch x + 2).
f ( x) → −f(x) → −f(x + 2) = h(x)
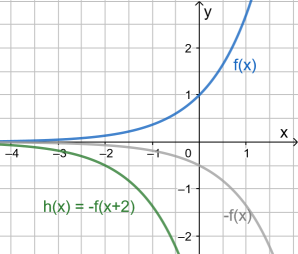
Beispiel 2
| = |
|
| = |
|
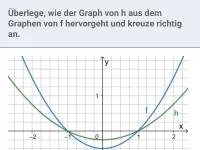
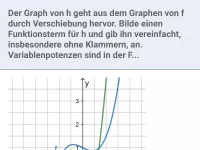
Welche Verschiebung(en)/Streckung(en)/Spiegelung(en) sind am Graphen von f durchzuführen, um den Graphen von h zu erhalten?
Lösung:
- mit Faktor 3 in y-Richtung strecken:
|
- um 5,5 nach oben verschieben:
|
- um 3 nach rechts verschieben:
|
- - - - - - - - - - - - - - - - - - - - -
Bemerkung: Den letzten Schritt könnte man auch an erster oder zweiter Stelle durchführen. Dagegen sind der erste und der zweite Schritt aufeinander abgestimmt. Vertauscht man sie (also erst nach oben verschieben, dann strecken), erhält man einen anderen Funktionsterm:
|
|
Das folgende Video zeigt ein weiteres Beispiel:

Lernvideo
Wie geht Gh aus Gf hervor (verschieben, strecken, spiegeln)
Kanal: Mathegym
Beispiel 3
| = |
|
| = |
|
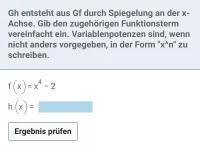
Welche Verschiebung(en)/Streckung(en)/Spiegelung(en) sind am Graphen von f durchzuführen, um den Graphen von h zu erhalten?
Lösung:
- mit Faktor 3 in y-Richtung strecken:
|
- um 5,5 nach oben verschieben:
|
- um 3 nach rechts verschieben:
|
- - - - - - - - - - - - - - - - - - - - -
Bemerkung: Den letzten Schritt könnte man auch an erster oder zweiter Stelle durchführen. Dagegen sind der erste und der zweite Schritt aufeinander abgestimmt. Vertauscht man sie (also erst nach oben verschieben, dann strecken), erhält man einen anderen Funktionsterm:
|
|
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
-
≈Oberstufe - Aufgaben + Stoff + Video
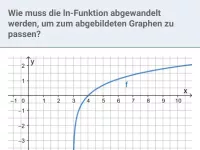
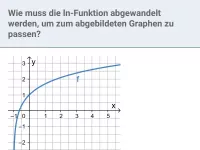
exp und ln - Verschiebung, Streckung und Spiegelung
Spiegelung des Graphen an der x- und y-Achse, Verschiebung in x- und y-Richtung, Streckung und Stauchung -
≈10. Klasse - Aufgaben + Stoff + Video
Graphen verschieben, spiegeln und strecken
Veränderungen des Funktionsterms und Auswirkungen auf den Funktionsgraphen -
≈0. Klasse - Aufgaben + Stoff + Video
kzo
keine Thematische Zuordnung
Ähnliche Themen
- Was ist bei Termen, die ausschließlich aus Summen bestehen, immer möglich?
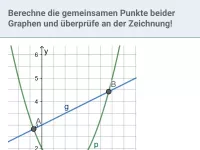
- Wie bestimmt man die Schnitt- und Berührpunkte zweier Graphen und welcher Spezialfall ist dabei zu beachten?
- Wie kann man die Einerstelle des Produkts zweier natürlicher Zahlen einfach bestimmen?
- Wie berechnet man einen Bruchteil einer Größe und wie wird das Ergebnis bezeichnet?
- Wie wird das bestimmte Integral geometrisch interpretiert?
- Wie bewirkt eine Veränderung des Funktionsterms f(x) eine Verschiebung des Graphen?
- Wie bewirkt man eine Spiegelung des Graphen einer Funktion an der x- oder y-Achse?
- Wie bewirkt man durch Änderung des Funktionsterms eine Spiegelung an der x-Achse oder y-Achse sowie eine Verschiebung in y-Richtung?
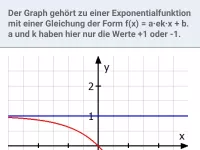
- Wie lautet die Gleichung der Asymptote bei Exponentialfunktionen vom Typ f(x) = a e^(kx) + b?
- Wie beeinflusst die Veränderung des Funktionsterms f(x) die Streckung/Stauchung des Graphen?