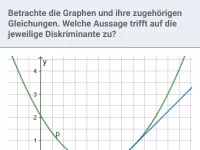
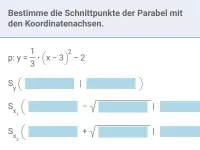
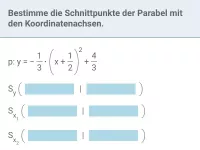
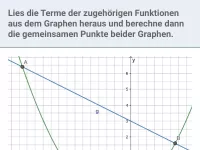
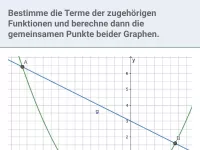
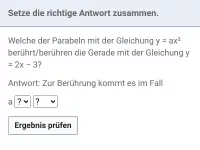
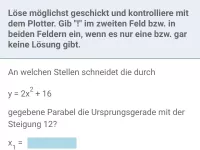
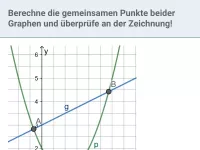
Wie bestimmt man die Schnitt- und Berührpunkte zweier Graphen und welcher Spezialfall ist dabei zu beachten?
Die Schnitt- und Berührpunkte (gemeinsame Punkte) zweier Graphen Gf und Gg ermittelt man durch Gleichsetzen ihrer Funktionsterme, also f(x) = g(x). Setze die Lösung der Gleichung in f(x) oder g(x) ein, um den zugehörigen y-Wert zu ermitteln.
Spezialfall f(x) = 0: Hier geht es um die gemeinsamen Punkte von Gf mit der x-Achse.
Beispiel
Bestimme die Schnittpunkte der beiden Parabeln p und q mit folgenden Gleichungen:
| = |
|
| = |
|
Lösung:
Zunächst setzt man die beiden Funktionsterme gleich und löst die quadatische Gleichung:
| = |
|
| |||||||||||||||||||||||||||||||||||||||||||
| = |
| ||||||||||||||||||||||||||||||||||||||||||||
Lösung mit Mitternachtsformel:
| = |
|
| = |
| |||||||||||||||||||||||||||||||||||
|
| = |
| |||||||||||||||||||||||||||||||||||
|
| = |
| |||||||||||||||||||||||||||||||||||
|
| = |
| |||||||||||||||||||||||||||||||||||
| = |
| |||||||||||||||||||||||||||||||||||
| = |
| |||||||||||||||||||||||||||||||||||
Lösung mit p-q-Formel:
| = |
|
| |||||||||||||||||
| = |
| ||||||||||||||||||
| = |
|
| = |
| |||||||||||||||||||||||||||||||||
|
| = |
| |||||||||||||||||||||||||||||||||
|
| = |
| |||||||||||||||||||||||||||||||||
|
| = |
| |||||||||||||||||||||||||||||||||
| = |
| |||||||||||||||||||||||||||||||||
| = |
| |||||||||||||||||||||||||||||||||
Schließlich setzt man die x-Werte in einen der beiden Funktionsterme ein, um den jeweiligen y-Wert des Schnittpunkts zu erhalten:
| = | 2,75 |
| = |
|
Beide Parabeln schneiden sich also in
und
.
|
|

Lernvideo
SCHNITTPUNKTE von Parabeln berechnen – Quadratische Funktionen gleichsetzen
Kanal: MathemaTrick
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
-
≈0. Klasse - Aufgaben + Stoff + Video
kzo
keine Thematische Zuordnung -
≈9. Klasse - Aufgaben + Stoff + Video
Quadratische Gleichungen - Schnittprobleme
Graphische Interpretation quadratischer Gleichungen; Bestimmung der Schnittpunkte von Parabeln bzw. Parabel und Gerade; Parameterbestimmung in Abhängigkeit von der Anzahl gemeinsamer Punkte
Ähnliche Themen
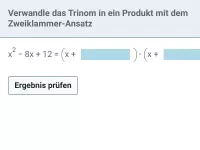
- Was ist bei Termen, die ausschließlich aus Summen bestehen, immer möglich?
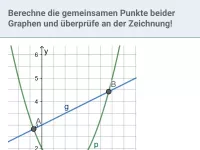
- Wie interpretiert man graphisch die Gleichungen f(x) = h(x) und f(x) = 0, und was bedeutet dies bei quadratischen Gleichungen?
- Wie kann man die Einerstelle des Produkts zweier natürlicher Zahlen einfach bestimmen?
- Wie berechnet man einen Bruchteil einer Größe und wie wird das Ergebnis bezeichnet?
- Wie kann man jede Gleichung graphisch lösen, wenn eine Lösung existiert?
- Wie kann eine Funktion f(x) abgewandelt werden, um ihren Graphen Gf zu strecken, stauchen, verschieben oder zu spiegeln?
- Wie wird das bestimmte Integral geometrisch interpretiert?
- Wie bestimmt man Schnitt- oder Berührpunkte zwischen einer Parabel und einer Geraden oder zwischen zwei Parabeln?
- Wie viele Nullstellen kann eine quadratische Funktion haben und wie bestimmt man diese?