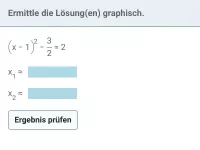
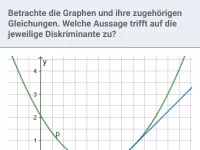
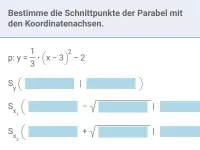
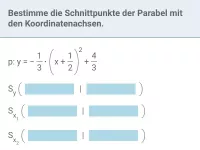
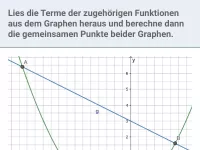
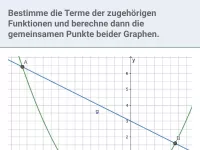
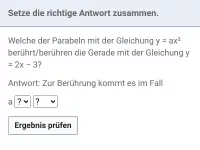
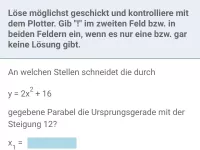
Wie bestimmt man Schnitt- oder Berührpunkte zwischen einer Parabel und einer Geraden oder zwischen zwei Parabeln?

Die Graphen zweier quadratischer Funktionen (Parabeln) oder einer quadratischen und einer linearer Funktion (Parabel und Gerade) f und g können sich zweimal schneiden, einmal berühren oder auch keine gemeinsamen Punkte aufweisen. Um das herauszufinden, setzt man beide Funktionsterme gleich, also f(x) = g(x), und bringt die Gleichung in die Normalform x² + px + q = 0. Mit Hilfe der Diskriminante D = (p/2)² − q bekommt man die Antwort:

  • D > 0 ⇔ zwei Schnittstellen
  • D = 0 ⇔ eine Berührstelle
  • D < 0 ⇔ weder Schnitt- noch Berührstelle, also keine gemeinsamen Punkte
Beispiel 1
- - - a) - - -
Gegeben sind eine Parabelschar 
p
a
 und eine Gerade g durch
p
a
 
x
=
ax
2
−
2x
+
1
g
 
x
=
3x
−
4
Gib jeweils den Wert oder die Werte für a an, bei dem sich 
p
a
 und g schneiden/berühren/weder schneiden noch berühren.

- - - b) - - -
Gegeben sind eine Parabel p und eine Geradenschar 
g
m
 durch
p
x
=
1
2
 
x
−
1
2
+
2
g
m
 
x
=
mx
−
2
Bestimme m so, dass sich Parabel und Gerade berühren.
Bei beiden Aufgaben muss man die Terme gleichsetzen und in die Nullform bringen, dann die Diskriminante ausrechnen!

- - - Zu a) - - -
ax
2
−
2x
+
1
=
3x
−
4
−
3x
+
4
ax
2
−
5x
+
5
=
0
:
a
 
a ist sicher nicht null
x
2
−
5
a
 
x
+
5
a
=
0
Berechnung der Diskriminante:
D
=
p
2
2
−
q
einsetzen
=
−
5
2a
2
−
5
a
=
25
4a
2
−
5
a
Bruchterme gleichnamig machen
=
25
4a
2
−
5
·
4a
a
·
4a
=
25
4a
2
−
20a
4a
2
zu einem Bruchterm
=
25
−
20a
4a
2
Untersuche jetzt die drei Fälle 
D
=
0
 (berühren), 
D
 
>
 
0
 (schneiden) und 
D
 
<
 
0
 (weder noch). Da das Vorzeichen von D nur vom Zähler abhängt (der Nenner 
4a
2
 ist garantiert positiv), verwenden wir für die weitere Untersuchung nur den Zähler von D:
D
=
0
25
−
20a
=
0
+
20a
25
=
20a
:
20
a
=
5
4
Bei 
a
=
5
4
 
berühren
 sich 
p
a
 und g.
D
>
0
25
−
20a
>
0
+
20a
25
>
20a
:
20
5
4
>
a
Bei 
a
 
<
 
5
4
 
schneiden
 sich 
p
a
 und g.
Bei 
a
 
>
 
5
4
 besitzen 
p
a
 und g keine gemeinsamen Punkte.

- - - Zu b) - - -
1
2
 
x
−
1
2
+
2
=
mx
−
2
binomische Formel
1
2
 
x
2
−
2x
+
1
+
2
=
mx
−
2
ausmultiplizieren
1
2
 
x
2
−
x
+
1
2
+
2
=
mx
−
2
−
mx
1
2
 
x
2
−
x
−
mx
+
2,5
=
−
2
+
2
1
2
 
x
2
−
x
−
mx
+
4,5
=
0
x ausklammern
1
2
 
x
2
−
1
+
m
 
x
+
4,5
=
0
·
2
x
2
−
2(1+m)x
+
9
=
0
Berechnung der Diskriminante:
D
=
p
2
2
−
q
D
=
−
1
+
m
2
−
9
D
=
m
2
+
2m
+
1
−
9
=
m
2
+
2m
−
8
Jetzt muss die Diskriminante gleich Null gesetzt werden (berühren heißt "genau eine Lösung"):
m
2
+
2m
−
8
=
0
pq
−
Formel
m
=
−
1
 
±
 
1
2
−
−
8
m
=
−
1±3
m
1
=
−
4
m
2
=
2
Parabelschar und Gerade - gegenseitige Lage in Abhängigkeit vom Scharparameter
Lernvideo

Parabelschar und Gerade - gegenseitige Lage in Abhängigkeit vom Scharparameter

Kanal: Mathegym
Beispiel 2
Gegeben sind die Parabel r und die Gerade g mit folgenden Gleichungen:
r: y
=
−
1
3
 
x
2
−
5x
+
7
g: y
=
5
6
 
x
−
2
a) Ermittle rechnerisch, ob sich beide Graphen schneiden, berühren oder ob Sie keine gemeinsamen Punkte aufweisen.
b) Falls es gemeinsame Punkte gibt: ermittle diese!
Zu a)
Setze dazu die beiden Funktionsterme gleich und bringe die quadratische Gleichung in die Normalform:
−
1
3
 
x
2
−
5x
+
7
=
5
6
 
x
−
2
−
5
6
 
x
+
2
−
1
3
 
x
2
−
5x
+
7
−
5
6
 
x
+
2
=
0
links zusammenfassen
−
1
3
 
x
2
−
35
6
 
x
+
9
=
0
·
−
3
x
2
+
35
2
 
x
−
27
=
0
Bestimme nun die Diskrimante D bzw. ihr Vorzeichen für 
p
=
35
2
 und 
q
=
−
27
:
D
=
p
2
2
−
q
p und q einsetzen
=
35
4
2
+
27
Da man nur das Vorzeichen von D wissen muss, um die Frage zu beantworten, kann man die Berechnung bereits hier abbrechen, da man sieht, dass D positiv ist. Aus 
D
 
>
 
0
 folgt, dass sich r und g in zwei Punkten schneiden.

Zu b)
Um die beiden Schnittpunkte zu ermitteln, muss D vollständig ausgerechnet werden, um die beiden Lösungen der quadratischen Gleichung mit der p-q-Formel bestimmen zu können:
x
1,2
=
−
q
2
 
±
 
D
einsetzen
=
−
35
4
 
±
 
D
Man erhält die beiden Lösungen 
x
1
 und 
x
2
, die mit Taschenrechnergenauigkeit (ANS-Taste) in eine der beiden Funktionsterme - vorzugsweise in g(x) - eingesetzt werden müssen, um die zugehörigen y-Werte zu ermitteln. Erst dann werden die beiden Schnittpunkte mit gerundeten Koordinaten angegeben:
S
1
 
−
18,9
 
|
 
−
17,8
 und 
S
2
 
1,4
 
|
 
−
0,8
graphik
Parabel und Gerade - gemeinsame Punkte - mit p-q Formel
Lernvideo

Parabel und Gerade - gemeinsame Punkte - mit p-q Formel

Kanal: Mathegym
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen