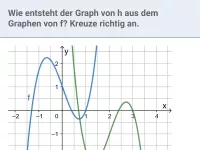
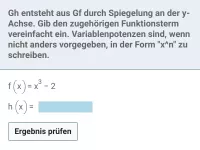
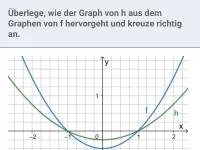
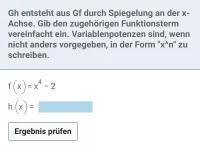
Wie beeinflusst die Veränderung des Funktionsterms f(x) die Streckung/Stauchung des Graphen?
Sei Gf der Graph einer Funktion f und a > 0.
- a·f(x)
bewirkt eine Streckung von Gf in y-Richtung mit dem Faktor a. Eine echte Streckung liegt im Fall a > 1 vor, im Fall 0 < a < 1 erhält man eine Stauchung. - f(a·x)
bewirkt eine Streckung von Gf in x-Richtung mit dem Faktor 1/a. Eine echte Streckung liegt im Fall 0 < a < 1 vor, im Fall a > 1 handelt es sich um eine Stauchung.
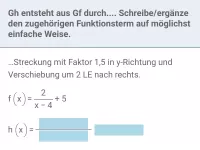
Beispiel
G | f |
a)
| = |
|
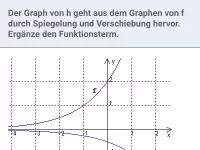
b)
| = |
|
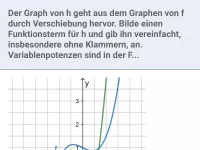
c)
| = |
|
Lösung zu (a)
…in y-Richtung:
| = |
|
…in x-Richtung:
| = |
|
Lösung zu (b)
…in y-Richtung:
| = |
|
…in x-Richtung:
| = |
|
Lösung zu (c)
…in y-Richtung:
| = |
|
…in x-Richtung:
| = |
|
Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
- Wie kann eine Funktion f(x) abgewandelt werden, um ihren Graphen Gf zu strecken, stauchen, verschieben oder zu spiegeln?
- Wie bewirkt eine Veränderung des Funktionsterms f(x) eine Verschiebung des Graphen?
- Wie bewirkt man eine Spiegelung des Graphen einer Funktion an der x- oder y-Achse?
- Was muss beachtet werden, wenn ein Funktionsgraph in dieselbe Richtung gestreckt und verschoben wird?