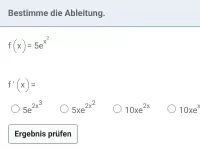
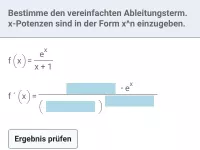
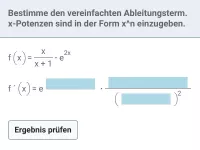
Wie lautet die Ableitung von f(x) = a·x^m und welche zwei Spezialfälle gibt es dazu?

Wenn f(x) = a · xm mit a ∈ ℝ und m ∈ ℤ \ {0}, dann ist
f ′(x) = a · m · x m−1.

Spezialfälle:

  • f(x) = a · x ⇒ f ´ (x) = a
  • f(x) = a ⇒ f ´ (x) = 0

Beispiel
f
 
x
=
1
2x
10
f ´
 
x
=
?
Lösung: Zunächst mal den Funktionsterm so umformen, dass x nicht mehr im Nenner auftritt:
f
 
x
=
1
2
·
x
−
10
Jetzt die Ableitungsregel anwenden:
f ´
 
x
=
1
2
·
−
10
·
x
−
11
=
−
5
·
x
−
11
Um negative Exponenten zu vermeiden, könnte man das Ergebnis auch schreiben als
f ´
 
x
=
−
5
x
11
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen