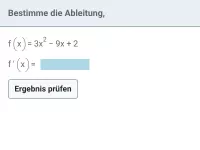
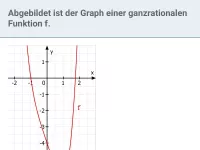
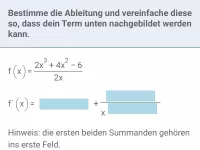
Was folgt für die Ableitung und jede Stammfunktion einer ganzrationalen Funktion mit ungeradem Grad und negativem Leitkoeffizienten?

Die Ableitung von a·xⁿ ist a·n·xⁿ⁻¹. Für ganzrationale Funktionen gilt daher:

Wenn f den Grad n besitzt, dann besitzt die Ableitung f´ den Grad n−1 und jede Stammfunktion F den Grad n+1. Insbesondere ist der Grad von f´ und F damit ungerade, falls der Grad von f eine gerade Zahl ist und umgekehrt.
Wenn der Leitkoeffizient von f(x), also der Faktor vor der höchsten x-Potenz, eine positive bzw. negative Zahl ist, dann gilt das auch für die Leitkoeffizienten von f´ und F.

Beispiel

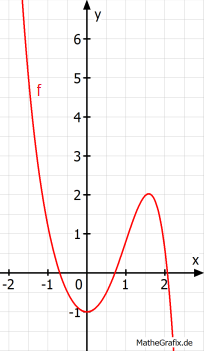
Abgebildet ist der Graph der ganzrationalen Funktion f. Setze den Term der Ableitung f´(x) richtig zusammen. Wähle dazu aus der ersten und letzten Spalte jeweils den passenden Teilterm aus (in der Mitte steht immer 4x).

f´(x)

−

Lösung:

Grad und Leitkoeffizient von f

Zunächst ist zu klären, ob der Grad von f eine gerade oder ungerade Zahl ist und ob der Leitkoeffizient von f(x) positiv oder negativ ist. Bei ganzrationalen Funktionen (Polynomfunktionen) lässt sich das am Verlauf des Graphen, woher er kommt und wohin er geht, leicht ablesen: Der abgebildete Graph "kommt von oben und geht nach unten", das bedeutet "Grad ungerade und Leitkoeffizient negativ". Du kennst die entsprechende Regel nicht oder hast sie vergessen? Im Kapitel "ganzrationale Funktionen" wird das genauer erklärt.

Grad und Leitkoeffizient von f´

Beim Ableiten einer ganzrationalen Funktion bleibt der Leitkoeffizient von f(x) vom Vorzeichen her gleich, was man anhand der Ableitungsregel sofort erkennt. Der Grad von f´ ist immer um eins kleiner als der von Grad von f. In diesem Fall können wir bzgl. f´(x) also schlussfolgern: "Grad geradzahlig und Leitkoeffizient ebenfalls negativ". Damit ist in der ersten Spalte

−

auszuwählen.