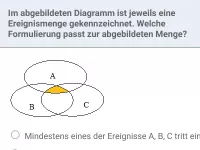
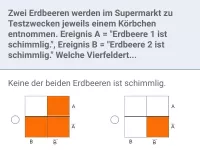
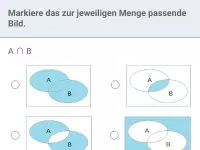
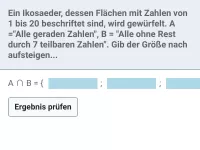
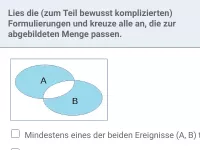
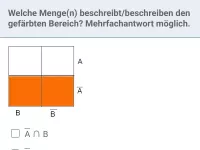
Wie lautet der Additionssatz für die Wahrscheinlichkeit von P(A ⋆ B)?
Nach dem Additionssatz gilt für beliebige Ereignisse A und B:
P( A ∪ B ) = P ( A ) + P ( B ) − P ( A ∩ B )
Alternativ berechnet man die "Oder-Wahrscheinlichkeit" wie folgt:P( A ∪ B ) = P( A ∩ B ) + P( B ∩ A ) + P( A ∩ B )
Beispiel 1
|
|
|
|
| |||||
|
|
|
| |||||
|
|
|
| |||||
|
|
|
|
|
| = | ?
|
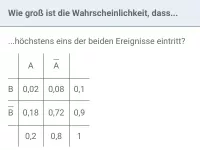
A ∪ B betrifft die drei unten markierten Felder der A-Spalte und der B-Zeile (ohne die Summen am Rand). Es gibt zwei Möglichkeiten, die Wahrscheinlichkeit zu bestimmen.
- Lösung auf direktem Wege
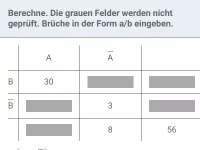
Ergänze die Vierfeldertafel und addiere dann die relevanten Felder (markiert):
|
|
|
|
| |||||
|
|
|
| |||||
|
|
|
| |||||
|
|
|
|
|
| = |
|
- Lösung mit Hilfe des Additionssatzes
Hier addiert man zur Spaltensumme von A die Zeilensumme von B und zieht dann das Feld, in dem sich Zeile und Spalte überlappen, ab:
| = |
| |||||||||||||||||||||||||||||||||
|
| = |
| |||||||||||||||||||||||||||||||||
|
| = |
| |||||||||||||||||||||||||||||||||
Hinweis: bei dieser Aufgabe ist der Additionssatz das etwas einfachere Verfahren, da die dafür notwendigen Zahlen direkt aus der Aufgabenstellung abgelesen werden können.
Beispiel 2
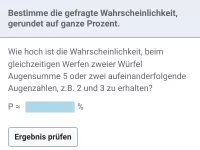
Wie hoch ist die Wahrscheinlichkeit, beim gleichzeitigen Werfen zweier Würfel Augensumme 6 oder zwei Augenzahlen zu erhalten, bei denen eine doppelt so groß wie die andere ist?
Lösung:
Insgesamt gibt es beim Werfen zweier Würfel 36 gleichwahrscheinliche Ergebnisse: 11, 12, …, 16, 21, 22, … 66.
A: Augensumme 6
Wird erfüllt durch die fünf Ergebnisse 15, 24, 33, 42 und 51.
P(A) | = |
|
B: eine Augenzahl doppelt so groß wie die andere
Wird erfüllt durch die sechs Ergebnisse 12, 24, 36, 21, 42 und 63.
P(B) | = |
|
A ∩ B
Die Schnittmenge von A und B besteht aus 24 und 42.
P(A ∩ B) | = |
|
A ∪ B
Nach dem Additionssatz gilt demnach:
| = |
|
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
- Was bedeutet es, wenn bei zwei Ereignissen A und B in der Stochastik "mindestens eines" oder "höchstens eines" eintritt?
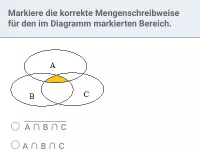
- Was sind Schnittmenge und Vereinigungsmenge und welche Symbole repräsentieren sie?
- Was ist in der Stochastik bezüglich des Begriffs "oder" zu beachten?
- Wie berechnet man die Wahrscheinlichkeit eines Ereignisses, wenn die Wahrscheinlichkeiten der Elementarereignisse bekannt sind?