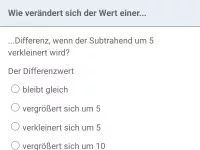
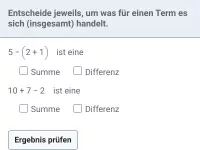
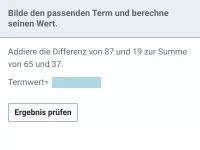
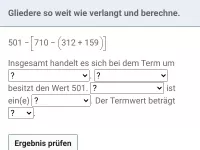
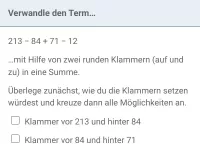
Was geschieht mit Summen und Differenzen, wenn alle Zahlen darin um denselben Betrag verändert werden?
Wird bei einer einfachen Summe jeder Summand um einen bestimmten Betrag vergrößert/verkleinert, so vergrößert/verkleinert sich der Wert des Terms um das Doppelte dieses Betrags.
Werden bei einer einfachen Differenz sowohl Minuend als auch Subtrahend um einen bestimmten Betrag vergrößert/verkleinert, so ändert sich der Termwert nicht.
Beispiel
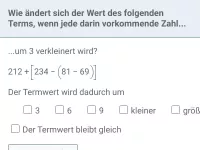
Wie verändert sich der Termwert, wenn jede darin vorkommende Zahl um 6 verkleinert wird?
(a)
23 | + | 7 |
(b)
23 | − | 7 |
(c)
190 | − |
|
(d)
1967 | − |
|
Lösung zu (a)
23 | + | 7 |
Der Termwert verringert sich um das Doppelte von 6, also um 12 (da Summe). Wer unsicher ist, kann das auch direkt nachrechnen:
| = | 30 |
| = | 18 |
Der Termwert hat sich von 30 auf 18, also um 12 verringert.
Lösung zu (b)
23 | − | 7 |
Der Termwert bleibt gleich (da Differenz). Wer unsicher ist, kann das auch direkt nachrechnen:
| = | 16 |
| = | 16 |
Lösung zu (c)
190 | − |
|
- Der Minuend (190) verringert sich um 6.
- Der Subtrahend, also die Summe in der runden Klammer, verringert sich um 12.
- Der Gesamtwert vergrößert sich damit um 6.
Wenn es dir schwerfällt, die Folgerung (Vergrößerung um 6) nachzuvollziehen, dann stell dir die Aufgabe als Gummibärchen-Aufgabe vor: "Minuend verringert sich um 6" bedeutet: in deiner Tüte sind 6 Gummibärchen weniger (als in einer anderen); "Subtrahend verringert sich um 12" bedeutet: aus der Tüte werden 12 Bärchen weniger herausgenommen (als aus der anderen); dann bleiben in deiner Tüte natürlich 6 Bärchen mehr als in der anderen.
Lösung zu (d)
| |||||||||||||||||||||
|
- Der Wert der runden Klammer bleibt gleich, da es sich um eine Differenz handelt.
- Der Minuend 95 verringert sich um 6.
- Damit erhöht sich der Wert der eckigen Klammer insgesamt um 6.
- Die Zahl 1967 verringert sich um 6.
- Zusätzlich wird (s.o.) um 6 mehr abgezogen.
- Der Gesamtwert reduziert sich also um 12.
Siehe auch