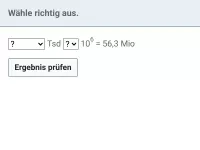
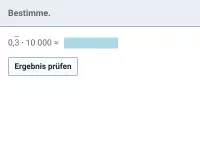
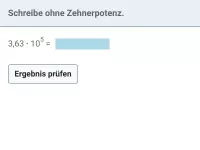
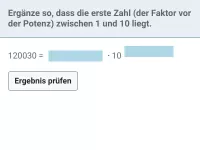
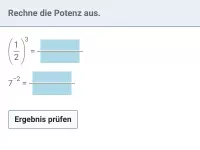
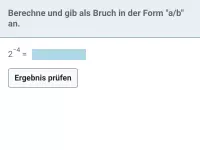
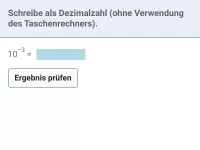
Was versteht man unter der wissenschaftlichen Notation einer Zahl?
In der Praxis werden sehr große oder sehr kleine Werte oft in der Form a · 10n geschrieben, wobei 1 ≤ a < 10.
Man spricht hier auch von wissenschaftlicher Notation.
Bei dieser Notation erkennt man anhand des Exponenten der Zehnerpotenz sofort die Größenordnung. Z.B. hat man bei 103 eine Zahl in der Größenordnung "Tausend". Bei 10-3 dagegen hat man eine Zahl in der Größenordnung eines Tausendstels.
Beispiel 1
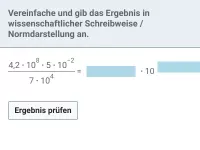
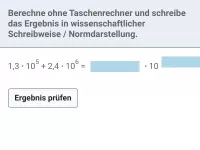
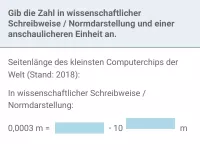
Schreibe in wissenschaftlicher Notation:
a) 5 723 000
b) 0,00095
Lösung:
- Sorge im ersten Schritt durch Kommaverschiebung dafür, dass die gegebene Zahl zwischen 1 und 10 liegt.
- Bei a) muss das Komma um 6 Stellen nach links verschoben werden, damit man 5,723000 (kürzer: 5,723) erhält
- Bei b) muss das Komma um 4 Stellen nach rechts verschoben werden, damit man 9,5 erhält.
- Gleiche im zweiten Schritt durch die entsprechende Zehnerpotenz aus: positiver Exponent bei Kommaverschiebung nach links, negativer Exponent bei Kommaverschiebeung nach rechts
- Bei a) muss also zum Ausgleich mit
10 | 6 |
10 |
|
Zusammenfassung:
5 723 000 | = |
|
0,00095 | = |
|
Beispiel 2
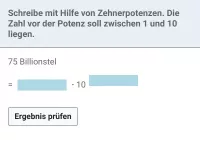
Schreibe "15 Millionstel" in wissenschaftlicher Notation.
Lösung:
15 Millionstel
= |
|
= |
|
Erläuterung:
, also ist ein Millionstel gleich
.15→1,5 bedeutet Kommaverschiebung um eins nach links, also muss die Zehnerpotenz zum Ausgleich um eins erhöht werden.
1 Million | = |
|
10 |
|
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
-
≈6. Klasse - Aufgaben + Stoff + Video
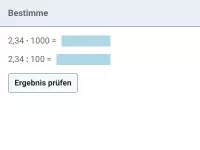
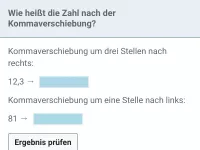
Dezimalzahlen - Multiplikation und Division mit Zehnerpotenzen
Terme berechnen und einfache Gleichungen lösen, bei denen mit/durch Zehnerpotenzen mutipliziert/dividiert wird. -
≈9. Klasse - Aufgaben + Stoff + Video
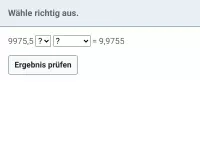
Potenzen - Normdarstellung
Potenzen in die Normdarstellung/wissenschaftliche Schreibweise umwandeln -
≈8. Klasse - Aufgaben + Stoff
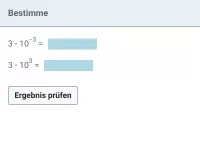
Potenzen mit negativen ganzzahligen Exponenten
Potenzen mit negativer Hochzahl richtig interpretieren und berechnen