Was ist der Differentialquotient und wie wird er berechnet?
Rechnerisch ergibt sich die lokale Änderungsrate an der Stelle x = a, indem man den den Grenzwert des Differenzenquotienten
[ f(x) − f(a) ] / (x − a)
für x → a (x ≠ a) bestimmt. Diesen Grenzwert (sofern er existiert) nennt man Differentialquotient.Beispiel 1
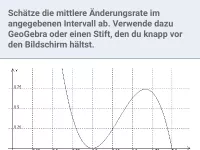
Berechne die lokale Änderungsrate an der Stelle x0.
| ; |
|
Lösung siehe Video:

Lernvideo
Lokales und globales Differenzieren, Differentialquotient, Beispiel
Kanal: Mathegym
Beispiel 2
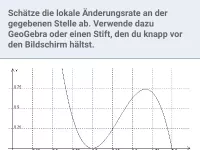
Berechne die lokale Änderungsrate an der Stelle
x | 0. |
| = | 2 |
- Differenzenquotient
| = |
| = |
| = |
| = |
|
- Differentialquotient
| = | 8 |
Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
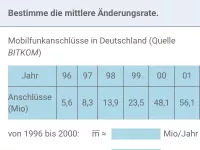
- Wie berechnet man die mittlere Änderungsrate einer Funktion und welcher synonyme Begriff ist dafür gebräuchlich?
- Wie lassen sich die mittlere und lokale Änderungsrate graphisch interpretieren?
- Wie ist der Zusammenhang zwischen dem Differenzenquotienten und der lokalen Änderungsrate?
- Wie bestimmt man die lokale Änderungsrate einer Funktion f an der Stelle x_0 mit Differenzenquotienten?