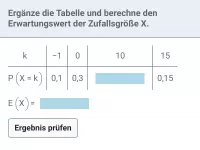
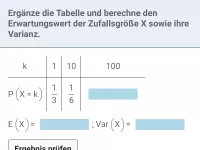
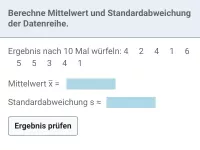
Was beschreiben Erwartungswert und Standardabweichung einer Zufallsgröße und wie berechnet man sie?
Erwartungswert und Standardabweichung einer Zufallsgröße X:
Erwartungswert μ(X) (lies:"mü von X"):
Der Erwartungswert beschreibt den Mittelwert der Zufallsgröße, sprich die Zahl, die die Zufallsgröße im Durchschnitt annimmt.
Berechnung des Erwartungswertes:
- Multipliziere jeden Wert xi von X mit der zugehörigen Wahrscheinlichkeit P(X=xi)
- Addiere alle so erhaltenen Werte.
- Als Formel: μ(X)=x1· P(X=x1)+ x2· P(X=x2) + ... + xn· P(X=xn)
Standardabweichung σ(X) (lies: "sigma von X")
Die Standardabweichung einer Zufallsgröße X gibt grob gesagt an, wie stark die Wahrscheinlichkeitsverteilung um den Erwartungswert gestreut ist.
Berechnung der Standardabweichung:
- Bestimme den Erwartungswert μ.
- Subtrahiere den Erwartungswert von jedem Wert xi den die Zufallsgröße annehmen kann.
- Quadriere jeweils die Ergebnisse.
- Multipliziere die Ergebnisse mit der zugehörigen Wahrscheinlichkeit.
- Addiere alle so erhaltenen Produkte.
- Ziehe vom Ergebnis die Quadratwurzel.
- Als Formel: σ(x) = √ Σ (xi − μ)2· P(X = xi)=√ [(x1 − μ)2· P(X = x1)+ (x2 − μ)2· P(X = x2) + ... + (xn − μ)2· P(X = xn)]
Beispiel
Paul hat sich ein Glücksspiel überlegt: Es wird mit einem Würfel gewürfelt. Beim Würfeln einer Quadratzahl erhält der Spieler 5 Euro, ansonsten muss der Spieler 2 Euro zahlen. Lässt du dich auf das Spiel ein? Berechne Erwartungswert und Standardabweichung und interpretiere.
| = | ? |
| = | ? |
Ein normaler Würfel hat zwei Quadratzahlen (1=12 und 4=22). Die anderen vier Zahlen (2, 3, 5 und 6) sind keine Quadratzahlen. Damit ergibt sich für die Zufallsgröße X: Gewinn in Euro folgende Tabelle:
|
|
| |||||||||||||||||
|
|
| |||||||||||||||||
|
|
Berechnung des Erwartungswertes:
| = |
| |||||||||||||||||||||||||||
|
| = |
| |||||||||||||||||||||||||||
μ (X) ≈ |
|
Berechnung der Standardabweichung:
| = |
| |||||||||||||||||||||||||||||||||||||||||||||||||
|
| = |
| |||||||||||||||||||||||||||||||||||||||||||||||||
|
| = |
| |||||||||||||||||||||||||||||||||||||||||||||||||
σ (X) ≈ |
|
Interpretation: Der Erwartungswert ist positiv. Daher ist auf lange Sicht ein (wenn auch nur kleiner) Gewinn von 0,30 Euro zu erwarten. Insofern kann man sich auf das Spiel einlassen. Allerdings ist die Standardabweichung (im Verhältnis zum Erwartungswert) groß. Dies bedeutet eine große Schwankung der Ergebnisse um den Erwartungswert. Es wäre daher riskant, den Erwartungswert als Gewinn-Vorhersage heranzuziehen.