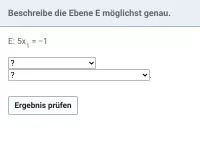
Welche Komponenten sind für die Normalengleichung einer Ebene notwendig?
Die allgemeine Normalengleichung der Ebene erhält man aus einem Normalenvektor und einem Aufpunkt P.
Beispiel
| = |
|
Die allgemeine Normalengleichung der Ebene lautet
| = |
|
n
| der Normalenvektor und |
p
| der Ortsvektor des Aufpunktes P ist. |
Setzt man die Werte ein, ergibt sich | : |
| = | 0 |
Durch Ausmultiplizieren erhalten wir die Koordinatengleichung der Ebene:
| = | 0 |
| = | 0 |
| = | 0 |
| = | 0 |
- - - - - - - - - - - - - - - - - -
Falls dich interessiert, WARUM die Ebenengleichung so berechnet werden kann, kannst du dir die Zeichnung anschauen und anhand dieser die Erklärung nachvollziehen:
|
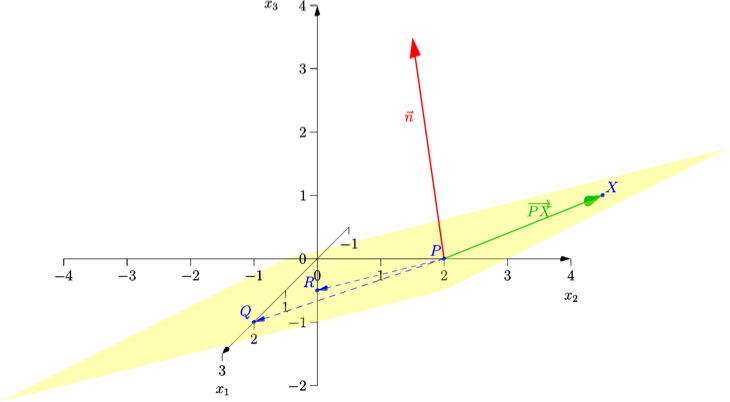
ebenso senkrecht zum Normalenvektor. Damit ist das Skalarprodukt beider Vektoren Null. Dies liefert die Normalengleichung der Ebene:
| = | 0 |
| = | 0 |
Bemerkung: Wenn nicht der Normalenvektor, sondern zwei weitere Punkte Q und R der Ebene gegeben sind (siehe Bild),
| ermittelt werden. |
Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
- Wie überprüft man, ob ein Punkt P in einer Ebene E in Koordinatenform liegt?
- Wie erkennt man, ob eine Ebene E in Koordinatenform durch den Ursprung geht oder zu einer Achse bzw. Ebene parallel ist?
- Wie leitet man die Normalenform einer Ebene aus drei gegebenen Punkten ab?
- Wie bestimmt man die Lage und Schnittgerade zweier Ebenen in Normalenform?
- Wie bestimmt man die Lage und Schnittgerade zweier Ebenen, wenn eine in Parameterform und die andere in Normalenform gegeben ist?
- Wie bestimmt man die Lage einer Geraden zu einer Ebene und findet einen Schnittpunkt?
- Wie kann man feststellen, ob zwei Ebenen parallel, senkrecht oder sich schneidend sind?
- Wie konstruiert man die Lotgerade zu einer Ebene und die Lotebene zu einer Geraden durch einen Punkt?
- Wie führt man Spiegelungen geometrischer Objekte an Geraden und Ebenen durch?