Was muss man beim Kürzen von Bruchtermen beachten?

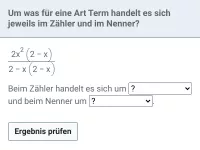
Ein Bruchterm lässt sich kürzen, wenn Zähler und Nenner (als Produkt dargestellt) in einem Faktor übereinstimmen. Das setzt, wie schon gesagt, Produkte auf beiden Seiten des Bruchstrichs voraus. Aus Summen oder Differenzen heraus darf nicht gekürzt werden!
Beispiel
Mit welchen Faktoren kann jeweils gekürzt werden?
6x
2
−
1
2x
2
  ;  
6x
·
x
−
1
2x
2
  ;   
6
 
x
−
1
2
2
 
1
−
x
  • Erster Bruchterm:
Man könnte meinen, dass mit 
2x
2
 gekürzt werden kann, denn im Zähler steht 
6x
2
=
3
·
2x
2
. Doch Vorsicht: es handelt sich im Zähler um eine Differenz! Daher kann nicht gekürzt werden.
  • Zweiter Bruchterm:
Hier liegt sowohl im Zähler als auch im Nenner ein Produkt vor. In beiden kommen jeweils die Faktoren 2 und x vor (Zähler: 
6x
=
3
·
2x
, Nenner: 
2x
2
=
2x
·
x
), also kann mit 
2x
 gekürzt werden.
  • Dritter Bruchterm:
6
 
x
−
1
2
=
2
·
3
·
1
−
x
2
Erläuterung: 
x
−
1
 und 
1
−
x
 unterscheiden sich nur durch das Vorzeichen, im Quadrat ergeben sie also denselben (positiven) Wert.
Zähler und Nenner sind also jeweils ein Produkt und enthalten jeweils die Faktoren 2 und 
1
−
x
. Also kann mit 
2
 
1
−
x
 gekürzt werden.
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen