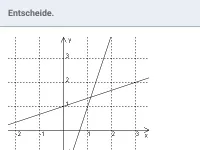
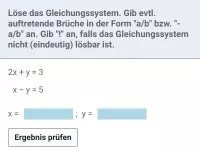
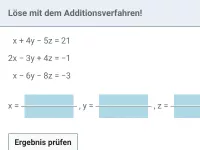
Welche drei Lösungsverfahren gibt es für Gleichungssysteme und was ist ihr Ziel?

Gleichungssysteme lassen sich z.B. mit Hilfe des Einsetzungsverfahrens, Gleichsetzungsverfahrens oder des Additionsverfahrens lösen. Alle Verfahren laufen darauf hinaus, Gleichungen mit jeweils nur einer Unbekannten zu erhalten, nach der man dann auflösen kann.
Beispiel 1

Löse mit Hilfe des Gleichsetzungsverfahrens:

I: x + 2y = − 6
II: x − y = 3
Lösung:
x
=
?
y
=
?
Hier ist es geschickt, beide Gleichungen nach x aufzulösen:
x
+
2y
=
−
6
−
2y
x
=
−
6
−
2y
und
x
−
y
=
3
+
y
x
=
3
+
y
Jetzt kann man die rechten Seiten der beiden Gleichungen gleichsetzen. Die Variable x fällt weg:
−
6
−
2y
=
3
+
y
Mithilfe von Äquivalenzumformungen löst man die Gleichung nach y auf:
−
6
−
2y
=
3
+
y
+
2y
−
6
=
3
+
3y
−
3
−
9
=
3y
:
3
−
3
=
y
y
=
−
3
y = −3 wird in die 1. oder 2. Gleichung eingesetzt, um x zu erhalten:
x
+
2
·
−
3
=
−
6
x
−
6
=
−
6
+
6
x
=
0
x
=
0
oder:
x
−
−
3
=
3
x
+
3
=
3
−
3
x
=
0
x
=
0
Lösung:
x
=
0
y
=
−
3
Beispiel 2

Löse mit Hilfe des Gleichsetzungsverfahrens:

I: y = 10x − 12
II: y = − 9x + 7
Lösung:
x
=
?
y
=
?
Da y in beiden Gleichungen auf der linken Seite alleine steht, kann man die rechten Seiten der Gleichungen gleichsetzen. Dadurch fällt y weg:
10x
−
12
=
−
9x
+
7
Diese Gleichung kann jetzt mithilfe von Äquivalenzumformungen nach x aufgelöst werden:
10x
−
12
=
−
9x
+
7
+
9x
19x
−
12
=
7
+
12
19x
=
19
:
19
x
=
1
x
=
1
x = 1 wird in die 1. oder 2. Gleichung eingesetzt, um y zu erhalten:
y
=
10
·
1
−
12
y
=
−
2
oder
y
=
−
9
·
1
+
7
y
=
−
2
Lösung:
x
=
1
y
=
−
2
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen