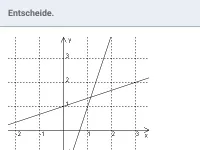
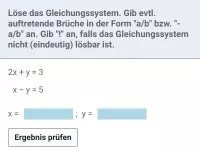
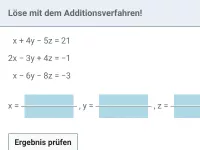
Welche Verfahren gibt es zum Lösen von Gleichungssystemen und was ist ihr Ziel?
Gleichungssysteme lassen sich z.B. mit Hilfe des Einsetzungsverfahrens oder des Additionsverfahrens lösen. Beide Verfahren laufen darauf hinaus, Gleichungen mit jeweils nur einer Unbekannten zu erhalten, nach der man dann auflösen kann.
Beispiel 1
Löse mit Hilfe des Einsetzungsverfahrens:
I: 2x + 3y = 5II: 3y − x = 0,5
Lösung: Löse (II) nach x auf und setze das Ergebnis in (I) für x ein. Dadurch fällt die Variable x weg.
| = |
|
| = |
| ||||||||||||||||||
| = |
| ||||||||||||||||||
| = |
|
| |||||||||||||||||
| = |
|
| |||||||||||||||||
| = |
| ||||||||||||||||||
| = |
| ||||||||||||||
| = |
| ||||||||||||||
Lernvideo
Lineare Gleichungssysteme, Einsetzverfahren, Beispiel
Kanal: Mathegym
Lernvideo
Gleichungssysteme lösen Einsetzungsverfahren – LGS lösen 2 Unbekannte
Kanal: MathemaTrick
Beispiel 2
Löse mit Hilfe des Additionsverfahrens:
I: 2x + 3y = 5II: 3y − x = 0,5
Lösung: Die Variable x fällt heraus, wenn man zu (I) das Doppelte von (II) addiert:
| I: | 2x + 3y = 5 |
| 2·II: | − 2x + 6y =1 |
| I + 2·II: | 9y = 6 |
Jetzt geht es weiter wie beim Einsetzverfahren (siehe vorausgehendes Beispiel).
Lernvideo
Kanal: Mathegym intern
Beispiel 3
Löse mit Hilfe des Additionsverfahrens:
| = | 5 |
| = | x |
Lösung siehe Video:

Lernvideo
Lineare Gleichungssysteme, Additionsverfahren, Beispiel 2
Kanal: Mathegym

Lernvideo
ADDITIONSVERFAHREN mit 2 Variablen – lineare Gleichungssysteme lösen
Kanal: MathemaTrick