Was bedeutet 'nicht differenzierbar an der Stelle x0' und welche Fälle gibt es?
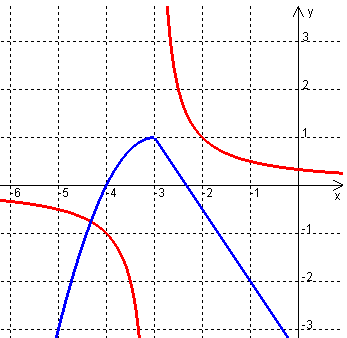
Nicht differenzierbar an der Stelle x0 kann z.B. bedeuten, dass der Graph einen Knick aufweist (blau) oder an der Stelle x0 überhaupt nicht definiert ist (rot), wie hier für x0 = -3 illustriert. Im Fall "blau" existieren aber die einseitigen Grenzwerte des Differenzialquotienten ("einseitige Tangentensteigungen"), nämlich 0 (linksseitig) und -3/2 (rechtsseitig).
Siehe auch






