Wie bestimmt man die Parameterform einer Ebene durch drei Punkte A, B und C?
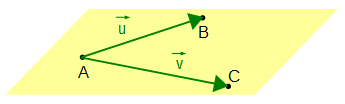
Ist eine Ebene durch drei Punkte A, B, C eindeutig definiert (d.h. die Punkte dürfen nicht alle auf einer Geraden liegen), so kann man z.B. A als Aufpunkt, den Vektor von A nach B als ersten und den Vektor von A nach C als zweiten Richtungsvektor für ihre Gleichung in Parameterform verwenden.
Beispiel
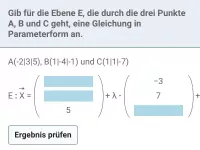
Gib für die Ebene E, die durch die drei Punkte A(2|0|0), B(1,5|2|0,5) und C(0|0|-2) geht, eine Gleichung in Parameterform an.
Lösung:
 |
|
Als Aufpunkt eignet sich A, als Richtungsvektoren eignen sich die beiden Vektoren, die A mit B und C verbinden, also
| = |
|
| = |
|
Da es bei den Richtungsvektoren weder auf Länge noch Orientierung ankommt, sollte man nach Möglichkeit Vereinfachungen vornehmen (oben markiert). Damit wird E durch folgende Gleichung in Parameterform beschrieben:
|
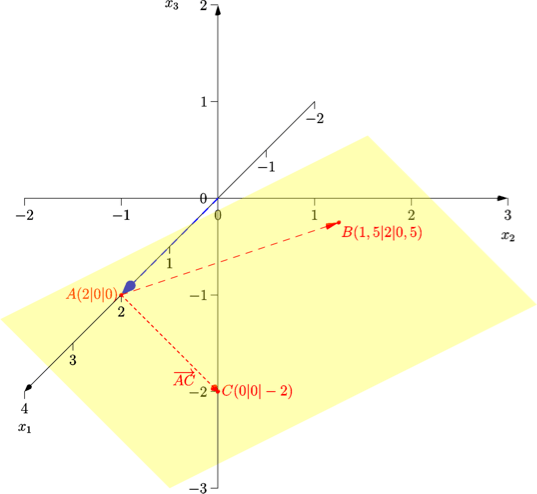
So würde man die Ebene zeichnen:
Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
- Wie legen zwei Geraden in Parameterform eine Ebene fest und wie bestimmt man deren Parameterform?
- Wie prüft man, ob ein Punkt P auf einer Ebene E in Parameterform liegt?
- Welche besonderen Lagebeziehungen zwischen einer Ebene und dem Koordinatensystem sind möglich und welche Rolle spielen dabei der Stützvektor und die Richtungsvektoren?
- Wie bestimmt man die Lagebeziehung und den Schnittpunkt einer Geraden und einer Ebene im Raum?