Wie prüft man, ob ein Punkt P auf einer Ebene E in Parameterform liegt?
Um zu prüfen, ob der Punkt P auf der Ebene E liegt, setzt man die Koordinaten von P in die Gleichung von E (Parameterform) ein. Sofern sich beide Parameter eindeutig bestimmen lassen, gilt P ∈ E.
Beispiel
| = |
|
Prüfe, ob der Punkt P(-1|3|5) auf E liegt.
Lösung: Setze zunächst die Koordinaten von P (unten markiert) in die Ebenengleichung ein:
| = |
|
Subtrahiert man noch auf beiden Seiten den (4|3|-4)-Ortsvektor und liest die entstehende Gleichung zeilenweise, so erhält man das Gleichungssystem:
| = |
|
(II) 0 | = |
|
(III) 9 | = |
|
Aus der zweite Gleichung folgt μ = 2λ, eingesetzt in (I) und (III) ergibt sich dann
| = |
|
(III´) 9 | = |
|
... und damit ein Widerspruch. Der Punkt P liegt also nicht in E.
Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
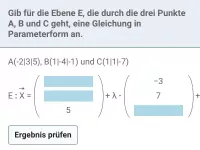
- Wie bestimmt man die Parameterform einer Ebene durch drei Punkte A, B und C?
- Wie legen zwei Geraden in Parameterform eine Ebene fest und wie bestimmt man deren Parameterform?
- Welche besonderen Lagebeziehungen zwischen einer Ebene und dem Koordinatensystem sind möglich und welche Rolle spielen dabei der Stützvektor und die Richtungsvektoren?
- Wie bestimmt man die Lagebeziehung und den Schnittpunkt einer Geraden und einer Ebene im Raum?