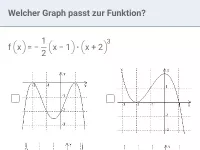
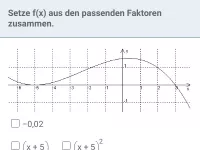
Was besagt der Satz vom Nullprodukt und was sind Vielfachheiten von Lösungen?
Der Satz vom Nullprodukt sagt:
Ein Produkt von zwei Zahlen ist genau dann null, wenn (mindetens) ein Faktor null ist.
In formalerer Schreibweise: Aus a·b = 0 folgt a = 0 und/oder b = 0 und umgekehrt.
Vielfachheit von Lösungen:
Die Gleichung (x − 1)2 = 0 hat nur die Lösung x = 1, da der Faktor (x − 1) aber zwei Mal auftritt, sagt man, dass x = 1 eine zweifache Lösung ist.
Entsprechend gibt es einfache, dreifache usw. Lösungen.
Beispiel
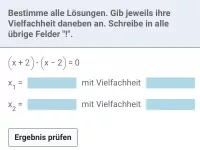
Löse die Gleichung.
| = | 0 |
Nach dem Satz vom Nullprodukt muss mindestens einer der beiden Faktoren Null sein. Man kann die Faktoren also einzeln Null setzen.
Aus (x-1) = 0 folgt x = 1 mit der Vielfachheit 1.
Aus (3x-5)² = 0 folgt x = 5/3 mit der Vielfachheit 2.
Ergebnisse:
| = |
|
Siehe auch