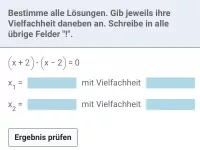
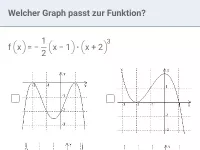
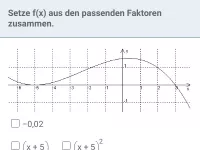
Wie beeinflusst die Vielfachheit einer Nullstelle das Verhalten des Graphen?

Die Vielfachheit einer Nullstelle wirkt sich auf das Verhalten des Graphen wie folgt aus
  • ungerade Vielfachheit (also einfach, dreifach, fünffach usw.) bedeutet, dass der Graph die x-Achse an der betreffenden Stelle schneidet ("Nullstelle mit Vorzeichenwechsel").
  • gerade Vielfachheit (also doppelt, vierfach, sechsfach usw.) bedeutet, dass der Graph die x-Achse an der betreffenden Stelle berührt ("Nullstelle ohne Vorzeichenwechsel").
Beispiel
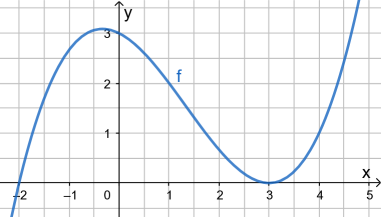
Gegeben ist folgender Graph 
G
f
 einer ganzrationalen Funktion vom Grad 3. Bestimme einen passenden Funktionsterm.
graphik
  • Von Nullstellen auf Linearfaktoren schließen
Da 
G
f
 die x-Achse an der Stelle 
x
=
−
2
 schneidet, kommt der Faktor 
x
+
2
 mit einer ungeraden Vielfachheit vor.
Da 
G
f
 die x-Achse an der Stelle 
x
=
3
 berührt, kommt der Faktor 
x
−
3
 mit einer geraden Vielfachheit vor.
Da die Funktion vom Grad 3 
=
1
+
2
 ist, kommt beim Faktor 
x
+
2
 nur der Exponent 1 und beim Faktor 
x
−
3
 nur der Exponent 2 in Frage:
f
 
x
=
a
·
x
+
2
·
x
−
3
2
 

  • Vorfaktor a bestimmen
G
f
 geht durch den Punkt (0/3). Setze diesen in die Funktionsgleichung ein, um den Vorfaktor a zu ermitteln:
y
=
a
·
x
+
2
·
x
−
3
2
Punkt (0/3) einsetzen
3
=
a
·
2
·
−
3
2
3
=
18a
:
18
a
=
1
6
Damit kann als passender Funktionsterm angegeben werden:
f
 
x
=
1
6
·
x
+
2
·
x
−
3
2
 
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen