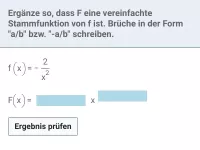
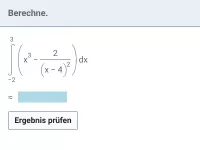
Wie findet man die Stammfunktion eines Bruchterms, wenn im Zähler die Ableitung des Nenners steht?
Ist f(x) ein Bruchterm und steht im Zähler der Ableitungsterm des Nenners, so lässt sich folgende Stammfunktion angeben:
f(x) = g'(x)/g(x) ⇒ F(x) = ln|g(x)|
Beispiel
Bestimme, falls möglich, eine Stammfunktion:
a)
f(x) | = |
|
b)
f(x) | = |
|
c)
f(x) | = |
|
Lösung: Beachte jeweils die Formel
| = |
|
Zu (a)
f(x) | = |
|
3 ist die Ableitung von
, also steht im Zähler die Ableitung des Nenners und damit lässt sich die Formel direkt anwenden:
ist ein Stammfunktion von f.
3x | + | 1 |
F(x) | = |
|
Zu (b)
f(x) | = |
|
Die Ableitung des Nenners ist
, im Zähler von f(x) steht allerdings nur die Hälfte davon, nämlich
. Um die Formel anwenden zu können, muss man hier also ein wenig umformen:
6x | + | 2 |
3x | + | 1 |
f(x) | = |
|
Jetzt hat der Bruchterm die Struktur, die er für die Formel oben benötigt. Den Ausgleichsfaktor 0,5 kann man dann einfach "mitnehmen":
ist ein Stammfunktion von f.
F(x) | = |
|
Zu (c)
f(x) | = |
|
Die Ableitung des Zählers ist
und somit vom Grad 2, während der Zähler vom Grad 1 ist. Hier kann man keine Umformung wie bei (b) vornehmen, insofern ist die Formel hier nicht anwendbar.
| − | 1 |
Weitere Beispiele zeigt das folgende Video ab 4:35.

Lernvideo
INTEGRATION von BRÜCHEN – gebrochen rationale Funktionen, Bruch, Integral – STAMMFUNKTION bilden
Kanal: MathemaTrick
Siehe auch